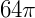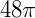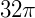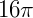Volume do cone - Geometria espacial - Matemática

Dado um cone de raio da base r e altura h. O seu volume (V) será:

$V = \frac{\pi \cdot r^2 \cdot h}{3}$

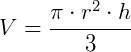
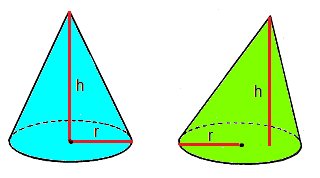É muito difícil demonstrar essa fórmula, mas o que devemos perceber dela é a seguinte ideia: o volume do cone é um terço do volume de um cilindro com mesma base e altura.

Ou seja: O volume de um cone de raio da base r e altura h é 1/3 do volume de um cilindro de raio da base r e altura h.

Exemplos:

1) Determine o volume de uma casquinha de sorvete (cone) com raio da base 4 cm e altura 10 cm (utilizar aproximação de π de 3,14).

Resposta:

r = 4 cm
h = 10 cm

$V = \frac{\pi \cdot r^2 \cdot h}{3}$

$V = \frac{\pi \cdot 16 \cdot 10}{3}$

$V = \frac{160\pi}{3} \approx 167,55 cm^3$

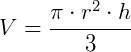
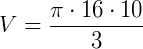
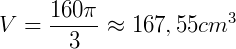
2) (FATEC-SP) A altura de um cone circular reto mede o triplo da medida do raio da base. Se o comprimento da circunferência dessa base é 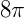$8\pi$ cm, então o volume do cone, em centímetros cúbicos, é:

a) $64\pi$
b) $48\pi$
c) $32\pi$
d) $16\pi$
e) $8\pi$

Resposta:

Deve-se lembrar, primeiramente, que o comprimento de uma circunferência de raio r se dá por: 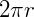$2\pi r$ . Segundo o enunciado, o comprimento da base é 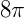$8\pi$ cm, logo: 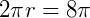$2\pi r = 8\pi$ , que significa que r = 4 cm.

Também segundo o enunciado, “a altura de um cone circular reto mede o triplo da medida do raio da base”, portanto, a altura será o triplo de 4 cm: h = 3 . 4 = 12 cm.

Já temos, então, todos os dados necessários para calcular o volume:

$V = \frac{\pi \cdot r^2 \cdot h}{3}$

$V = \frac{\pi \cdot 16 \cdot 12}{3}$

$V = \frac{192\pi}{3} = 64\pi$

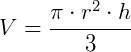
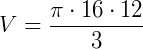
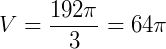
Assim, a alternativa correta é letra "a".