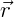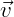Imagine um corpo em movimento. Por exemplo, um carro em uma estrada a certa velocidade. Durante o movimento, podemos associar as grandezas massa e velocidade desse carro – afinal, são fatores que interferem no desempenho do carro, como o tempo para frear, acelerar ou como esse carro interage com outra massa durante uma colisão. Esse é o conceito de quantidade de movimento. Agora, imagine um planeta (a Terra) girando em torno do Sol. Neste caso, também temos um corpo com determinada massa realizando um movimento; no entanto, agora é de rotação, em volta de um eixo fixo. Desse modo, esse movimento tem uma determinada velocidade angular associada a ele. E essa relação entre massa e velocidade angular gera uma grandeza chamada momento angular. É um conceito um tanto abstrato, no entanto é muito útil para descrever o movimento e a estabilidade de um corpo.
Podemos imaginar também uma bicicleta em movimento. Os pedais realizam um movimento em torno de um eixo fixo. E, enquanto pedalamos a bicicleta (ou a Terra gira em torno do Sol), o equilíbrio se mantém.
Assim, o momento angular (L) é um vetor perpendicular à quantidade de movimento associada a um corpo em movimento de rotação em torno de um ponto fixo.
O momento angular (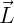 ) é dado por:
) é dado por:
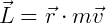
Onde:
 é o vetor raio entre o objeto e o eixo de rotação;
é o vetor raio entre o objeto e o eixo de rotação;- m é a massa do objeto;
 é o vetor velocidade linear do objeto.
é o vetor velocidade linear do objeto.
O vetor velocidade não pode ser paralelo ao vetor raio. Isso indicaria que o objeto não está fixo ao eixo de rotação e, assim, não teria momento angular.
O momento linear também pode ser dado em termos da velocidade angular do objeto:
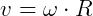
Ou
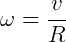
Para facilitar, vamos que os vetores velocidade e raio estão perpendiculares:
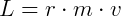
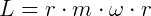
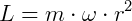
Quando falamos de corpos em movimento circular, podemos relacionar a sua distribuição de massa no corpo e como essa distribuição se relaciona com o raio do movimento. Essa grandeza se chama momento de inércia (I), e é dado por:
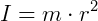
Assim, podemos escrever que o momento angular é dado por:
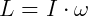
Na forma vetorial:
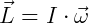
Referência:
Fundamentos da Física. Halliday, Resnik, Krane, Denneth. Vol. 01. LTC. 04ª Ed. RJ. 1996
Texto originalmente publicado em https://www.infoescola.com/mecanica/momento-angular/