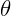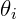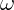Movimento circular

Um movimento uniforme é aquele onde um objeto percorre distâncias iguais em intervalos de tempos iguais. Quando essa trajetória é circular, temos o Movimento Circular Uniforme (MCU). Neste caso, como o é um círculo e há uma distância percorrida em intervalos iguais, o movimento é periódico, cíclico.

O período (T) significa o intervalo de tempo de um ciclo e a frequência (f) é quantos ciclos são realizados em uma unidade de tempo. Assim:

$f = \frac{1}{T}$

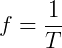
ou

$T = \frac{1}{f}$

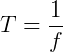
No movimento uniforme, as distâncias percorridas são lineares e no movimento circular, além de trajetória linear, o objeto descreve um ângulo θ, formando um círculo de raio R. O ângulo θ é dado em radianos e se relaciona com o espaço linear descrito e o raio R do círculo.

$S = \theta \cdot R$

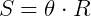
Ou

$\theta = \frac{S}{R}$

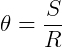
Assim, da função horária do espaço, temos:

$S = S_i + v \cdot t$

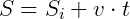
Da relação com o raio:

$\frac{S}{R} = \frac{S_i}{R} + \frac{v}{R} \cdot t$

$\theta = \theta_i + \omega \cdot t$

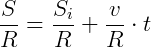
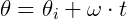
Onde:

• $\theta$ é o espaço angular final;
• $\theta_i$ é o espaço angular inicial;
• $\omega$ é a velocidade angular nessa trajetória.

Lembrando que o espaço angular é dado em radianos (rad). Então, a velocidade angular é dada é rad/s.

Se o objeto completa uma volta inteira, a espaço é dado por 2π. Então, a posição inicial é zero e o tempo é o mesmo que um período (T) – o objeto realiza um ciclo em uma unidade de tempo.

Então:

$2\pi = 0 + \omega \cdot T$

$\omega = \frac{2\pi}{T}$

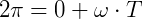
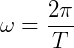
Ou, da relação com a frequência:

$\omega = 2\pi f$

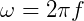
Referência:

Os Fundamentos da Física – Moderna Plus. Ramalho, Nicolau e Toledo. Vol. 01. Moderna. 11ª Ed. SP. 2016

Texto originalmente publicado em https://www.infoescola.com/mecanica/movimento-circular/