Ingressar na carreira acadêmica, apesar de parecer fácil para alguns, não é tarefa simples. Se já era complicada a entrada através do vestibular tradicional, que mais exigia conteúdos decorados do que a compreensão e aplicação dos diversos aspectos inerentes aos vastos campos do conhecimento, hoje o candidato a uma vaga num curso acadêmico poderá optar pelo Enem, sendo este alicerçado em diretrizes que cobram interpretação, raciocínio lógico, compreensão de mundo e de sociedade, transdisciplinaridade, ou seja, um conhecimento global, que se entrelaça nos vários componentes curriculares estudados ao longo da educação básica escolar.
Este trabalho é fruto de um levantamento estatístico realizado nos anos de 2011 e 2012 do Enem com vista a indicar aos futuros candidatos os principais temas cobrados no exame referente à matemática. Dessa forma, o candidato “deverá” estudar toda matemática básica dos ensinos fundamental e médio, mas poderá, se preferir, dar ênfase às áreas da matemática que mais foram cobradas nos dois últimos anos do Enem, pois, ao se manter a prioridade sobre algumas áreas específicas da matemática no exame, parece-se uma boa indicação de quais assuntos priorizar nos estudos para poupar tempo e rumar ao sucesso nesta área do conhecimento.
Conteúdo deste artigo
Áreas da matemática mais cobradas no Enem
Sempre com foco nos conhecimentos interdisciplinares e, por que não dizer transdisciplinares, o Enem deu forte atenção a algumas áreas específicas da matemática nos anos de 2011 e 2012. Considerando a grande possibilidade de esse fato recorrer você, candidato, poderá dar grandes passos no preparo para lidar com essas questões.
- Estatística - essa extensa área da matemática liderou as últimas edições do Enem, ocupando aproximadamente 17% (15 questões) do total de questões das duas provas do exame.
- Razões e Proporções – esta área liderou, juntamente com a estatística, as duas últimas edições do Enem com o mesmo percentual (~ 17%) e número de questões (15).
- Funções – também fortemente cobradas, as funções apareceram num percentual bastante considerável de aproximadamente 12%, num número de 11 questões.
- Análise combinatória e probabilidade – na mesma posição que as funções, essa grande área da matemática aparece com o mesmo percentual (~ 12%) e número de questões (11).
- Geometria plana, espacial e analítica – a primeira aparece em um número considerável de 10 questões, representando um percentual aproximado de 11%; a geometria espacial aparece em 08 questões, aproximadamente 9% e a geometria analítica em apenas 01 questão, ~ 1%.
- Matemática financeira – esta aparece em um número total de 06 questões, ou seja, ~ 7%.
- Trigonometria e Operações com Unidades Medidas – ambas, apesar de não se relacionar diretamente, aparecem com o mesmo número de questões (04) e, portanto, mesmo percentual (~ 4%).
- Progressões, matrizes, valor posicional e logaritmo - essas áreas muito pouco aparecem; a primeira, 01 questão, ~ 1%; a segunda, 01 questão, ~ 1%; a terceira, 02 questões, ~ 2% e a quarta, 01 questão, ~ 1%.
Analisando o gráfico
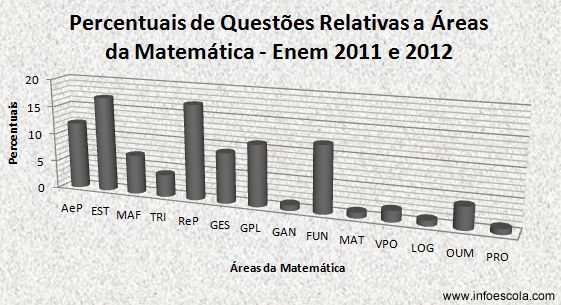
Para melhor visualizar os dados dispostos acima, elaboramos o gráfico mostrado na sequência, onde o candidato poderá perceber a importância de se estudar mais, ou “menos”, determinada área do conhecimento matemático (os valores percentuais do gráfico encontram-se arredondados, por motivo de conveniência matemática).
- AeP → Análise Combinatória e Probabilidade
- EST → Estatística
- MAF → Matemática Financeira
- TRI → Trigonometria
- ReP → Razões e Proporções
- GES → Geometria Espacial
- GPL → Geometria Plana
- GAN → Geometria Analítica
- FUN → Funções
- MAT → Matriz
- VPO → Valor Posicional
- LOG → Logaritmo
- OUM → Operações com Unidades de Medidas
- PRO → Progressões
Certamente o candidato pôde perceber, através do gráfico de barras acima, as principais áreas da matemática cobradas nas duas últimas realizações do Enem. Visivelmente destacam-se: Estatística, Razões e Proporções, Análise Combinatória e Probabilidade, Funções e Geometria Plana e Espacial.
Como estudar matemática para o Enem
Não há fórmula mágica que possa nos conduzir ao sucesso, mas sim trabalho duro, persistência, otimismo, motivação, dedicação e planejamento. Confira as dicas abaixo:
- Comece abrindo mão daquilo que é dispensável a sua vida cotidiana para que sobre mais tempo para os seus estudos;
- Forme grupo de estudos com colegas que também irão passar pelo crivo do Enem, assim vocês poderão tirar dúvidas entre si e compartilhar as descobertas que facilitarão à realização da prova, mas lembre-se, o foco do grupo de estudos é adquirir e aperfeiçoar conhecimentos e não discutir sobre a vida pessoal de seus membros;
- Se algo parecer incompreensível, não desista, busque ajuda com um professor de matemática.
- Seja otimista, acredite em sua capacidade. Saiba que tudo é possível àqueles que se dedicam e acreditam em si mesmo;
- Procure se motivar vendo os principais benefícios do ingresso na carreira acadêmica. Tente vê-se estudando o curso desejado, tente vê-se ocupando um lugar no mercado de trabalho como fruto da realização acadêmica, veja-se melhor financeiramente, passeando, realizando sonhos, motive-se;
- Estude o quanto puder durante o dia, mas com intervalos de 30 minutos para descanso. Lembre-se que se você estiver cansado, com fome ou sono, sua produtividade será bastante reduzida, sendo assim, divida o seu dia em blocos de estudos com intervalos entre eles, se alimente bem, durma bem, se revigore para reiniciar uma nova maratona de estudos;
- Planeje bem os seus estudos, selecione as disciplinas que serão estudadas mais tempo e as que serão estudadas menos tempo, sempre se lembrando de dar mais atenção às disciplinas da área de exatas, devido à complexidade, bem como a língua portuguesa e redação, devido ao peso das questões. Faça um cronograma de estudos e mantenha a mão um cronômetro dividindo o tempo de cada disciplina. Não se esqueça de reservar intervalos de tempo para o descanso e para alimentação, enfim, planeje seus estudos de acordo com a sua disponibilidade.
Considerações finais
Gostaria de deixar claro que não quero, com este trabalho, direcionar os candidatos unicamente para as questões destacadas neste texto. Apenas disponibilizo aos interessados um levantamento estatístico muito curioso em relação ao Enem que, a meu ver, pode sim ser usado para melhor direcionar os estudos desse exame no que se refere à matemática.
Claro que, se o candidato tiver disponibilidade, deverá estudar todos os conteúdos relativos à matemática da educação básica, pois isso lhe daria segurança para resolver quaisquer que seja o conhecimento cobrado nas questões dispostas no exame, porém, aos que não têm tanto tempo para estudar, ou até mesmo aos que têm, vejo como importante o norteamento dos estudos, desde que embasado em conhecimento científico, como é o caso deste trabalho.
“Aos que persistem, reserva-se o sucesso.” (Robison Sá)
Referência bibliográfica
INEP. Provas e Gabaritos. Disponível em: http://inep.gov.br/web/enem/edicoes-anteriores/provas-e-gabaritos.
Texto originalmente publicado em https://www.infoescola.com/educacao/matematica-no-enem/