Progressões

O termo “progressão” remete a um desenvolvimento gradual de um processo ou uma sucessão. Em matemática, dizemos que esta sucessão é uma sequência. Podemos exemplificar algumas sequências conhecidas:

• Sequência das eleições para presidente a partir de 1994: (1994, 1998, 2002, 2006, 2010, 2014, 2018);
• Sequência das edições copa do mundo a partir de 1990: (1990, 1994, ..., 2014, 2018);
• Sequência dos números naturais: (0, 1, 2, 3, 4, 5, ...)

Note que em todos os exemplos acima, as sequências são definidas por uma ordem em seus elementos (também chamados de termos). Definimos o tamanho de uma sequência pelo número de termos que ela possui, o que nos traz a possibilidade de que ela seja infinita ou finita.

Em uma sequência, finita ou infinita, nomeamos os termos em função de sua posição, ou seja, nos exemplos acima temos que o 1º termo de cada um são: 1994, 1990 e 0. O segundo termo: 1998, 1994 e 1. Assim, determinamos que um termo de uma sequência em função de sua posição pode ser chamado de a_n, onde n representa a sua posição (1ª, 2ª, 3ª, ..., nª). Dizemos também que o primeiro e o último termo de uma sequência finita (a₁ e a_n) são chamados de extremos de uma sequência. Podemos então representa-la de uma forma genérica:

Definição formal de Sequência Numérica: “Uma sequência numérica é uma função f, definida no conjunto dos números naturais, ou inteiros positivos tal que: 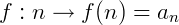$f:n\rightarrow f(n)=a_n$. Onde o n é chamado de índice e 𝑎_𝑛 o n-ésimo elemento da sequência, ou termo geral”.

(𝑎₁, 𝑎₂, 𝑎₃, 𝑎₄, 𝑎₅, … , 𝑎_𝑛)</span>

Progressão aritmética

Vamos supor, por hora, a sequência dos números naturais: Cada termo, iniciando com 0(a₁) é obtido somando 1 ao seu anterior. Ou seja:

𝑎₂ = 𝑎₁ + 1 = 1

𝑎₃ = 𝑎₂ + 1 = (𝑎₁ + 1) + 1 = 2

𝑎₄ = 𝑎₃ + 1 = (𝑎₂ + 1) + 1 = [(𝑎₁ + 1) + 1] + 1 = 3

...

No caso da sequência dos números naturais, o número 1 que é somado a cada termo é chamado de razão da progressão (r). Em uma progressão aritmética (P.A), cada termo de uma sequência é a soma do elemento anterior com sua razão. Vamos agora reescrever os termos da sequência em função de r (razão).

𝑎₂ = 𝑎₁ + r

𝑎₃ = 𝑎₂ + r = (𝑎₁ + r) + r = 𝑎₁ + 2r

𝑎₄ = 𝑎₃ + r = (𝑎₂ + r) + r = [(𝑎₁ + r) + r] + r = 𝑎₁ + 3r

...

Ora, se continuarmos realizando esta operação para os próximos termos, encontramos então uma fórmula para determinar o termo geral 𝑎_𝑛 de uma progressão aritmética, que será dado por:

$a_n=a_1+(n-1)r$

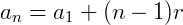
Progressão geométrica

Assim como em uma P.A., a Progressão Geométrica (P.G) também é representada por uma sequência, porém seus elementos são dados pelo produto do termo anterior por uma constante que chamaremos de razão q. Em outras palavras, dada a sequência:

(𝑎₁, 𝑎₂, 𝑎₃, 𝑎₄, 𝑎₅, … , 𝑎_𝑛)

Temos que:

𝑎₂ = 𝑎₁ . q

𝑎₃ = 𝑎₂ . q = (𝑎₁ . q) . q = 𝑎₁ . q²

𝑎₄ = 𝑎₃ . q = (𝑎₂ . q) . q = [(𝑎₁ . q) . q ] . q = 𝑎₁ . q³

...

Naturalmente, se quisermos obter a razão de uma P.G., devemos dividir um termo pelo seu anterior, assim:

$q=\frac{a_2}{a_1}=\frac{a_3}{a_2}=\frac{a_4}{a_3}=...=\frac{a_n}{a_{n-1}}$

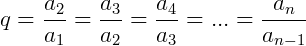
Ao continuarmos a operação para determinar um termo 𝑎𝑛 qualquer em uma P.G., obtemos então a fórmula do termo geral:

$a_n=a_1\cdot q^{n-1}$

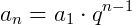
Referências Bibliográficas:

DANTE, Luiz Roberto. Matemática: Contextos & Aplicações - Volume 1. São Paulo: Editora Ática, 2011.

ÁVILA, Geraldo. Introdução à Análise Matemática. São Paulo: Blucher, 1999.

Texto originalmente publicado em https://www.infoescola.com/matematica/progressoes/