O estudo do logaritmo surgiu, sobretudo, como um auxílio na solução de equações exponenciais. Ele está presente, também, em modelos matemáticos utilizados várias áreas. Em Química, por exemplo, ele está presente no cálculo de pH e pOH. A escala Richter, por exemplo, é uma escala logarítmica arbitrária, de base 10, utilizada para quantificar a magnitude de um terremoto.
Conteúdo deste artigo
Definição
Sendo a e b números reais positivos, chama-se logaritmo de b na base a, o expoente em que a deve ser elevado de modo que a potência obtida de base a seja igual a b.
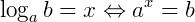
Com 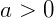 ,
, 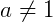 e
e 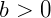
Assim, o logaritmo nada mais é que um expoente. Dizemos que "a" é a base do logaritmo, "b" é o logaritmando e "x" é o logaritmo.
Exemplo: 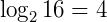 , pois
, pois 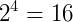 .
.
Definições
I) O logaritmo cujo o logaritmando é igual a 1 e a base é qualquer, é igual a zero:
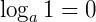 , pois
, pois 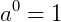
II) O logaritmo cujo a base e o logaritmando são iguais é igual a um:
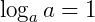 , pois
, pois 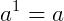
III) A potência de base "a" e expoente 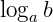 é igual a b:
é igual a b:
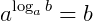
IV) Dois logaritmos são iguais, numa mesma base, se os logaritmandos são iguais:
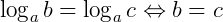
Propriedade dos logaritmos
1. Logaritmo do produto
O logaritmo do produto de dois fatores "a" e "b", em qualquer base "c", é igual à soma dos logaritmos de cada um desses fatores.
Se c > 0 e 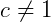 , a > 0, b > 0, então:
, a > 0, b > 0, então:
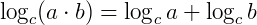
Exemplo: 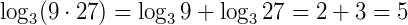
2. Logaritmo do quociente
O logaritmo do quociente de dois fatores a e b, em qualquer base c, é igual à diferença dos logaritmos de cada um desses fatores.
Se c > 0 e 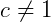 , a > 0, b > 0, então:
, a > 0, b > 0, então:
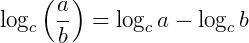
Exemplo: 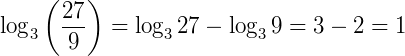
3. Logaritmo da potência
O logaritmo de uma potência, em qualquer base c, é igual ao produto entre o expoente da potência e o logaritmo cujo logaritmando é a base da potência.
Se a > 0 e 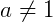 , b > 0,
, b > 0, 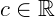 , então:
, então:
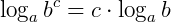
Exemplo: 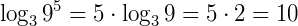
4. Logaritmo de uma raiz
O logaritmo da raiz enésima de um número real positivo é o produto entre o inverso do índice da raiz pelo logaritmo cujo o logaritmando é o radicando:
Se a > 0 e 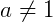 , b > 0,
, b > 0, 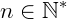 , então:
, então:
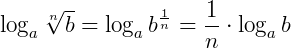
Exemplo: 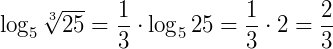
Mudança de Base
Algumas vezes, os logaritmos com bases diferentes precisam ser transformados para outra base, de forma que ela seja a mesma para ambos.
Se a, b e c são números reais positivos, então:
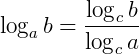 ,
, 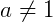 e
e 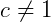
Exemplo: 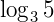 transformado para a base 2 fica:
transformado para a base 2 fica:
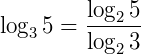
Se a e b são reais positivos e quisermos transformar 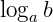 para a base b, temos:
para a base b, temos:
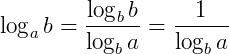 ,
, 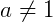 e
e 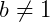
Exemplo: 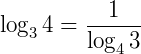
Se a e b são reais positivos, temos que:
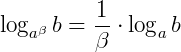 ,
, 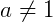 e
e 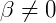
Exemplo: 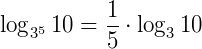
Leia também:
Referência:
DOLCE, Osvaldo; IEZZI, Gelson; MURAKAMI, Carlos. Fundamentos de Matemática Elementar. Logaritmos. Vol. 2. São Paulo: Atual, 1997.
Texto originalmente publicado em https://www.infoescola.com/matematica/logaritmo/