O cologaritmo é um termo utilizado para auxiliar cálculos envolvendo logaritmos. Para compreender, vamos relembrar alguns conceitos importantes dos logaritmos.
Conteúdo deste artigo
Definição de Logaritmo
Sendo a e b números reais positivos, chama-se logaritmo de b na base a, o expoente em que a deve ser elevado de modo que a potência obtida de base a seja igual a b.
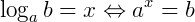
Com 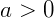 ,
, 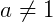 e
e 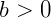 .
.
Assim, o logaritmo nada mais é que um expoente. Dizemos que a é a base do logaritmo, b é o logaritmando e x é o logaritmo.
Propriedades dos Logaritmos
1. Logaritmo do produto
O logaritmo do produto de dois fatores "a" e "b", em qualquer base "c", é igual à soma dos logaritmos de cada um desses fatores.
Se c > 0 e 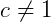 , a > 0, b > 0, então:
, a > 0, b > 0, então:
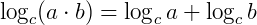
Exemplo: 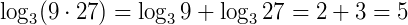
2. Logaritmo do quociente
O logaritmo do quociente de dois fatores a e b, em qualquer base c, é igual à diferença dos logaritmos de cada um desses fatores.
Se c > 0 e 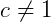 , a > 0, b > 0, então:
, a > 0, b > 0, então:
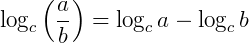
Exemplo: 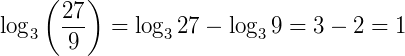
3. Logaritmo da potência
O logaritmo de uma potência, em qualquer base c, é igual ao produto entre o expoente da potência e o logaritmo cujo logaritmando é a base da potência.
Se a > 0 e 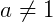 , b > 0,
, b > 0, 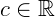 , então:
, então:
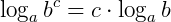
Exemplo: 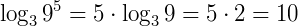
4. Logaritmo de uma raiz
O logaritmo da raiz enésima de um número real positivo é o produto entre o inverso do índice da raiz pelo logaritmo cujo o logaritmando é o radicando:
Se a > 0 e 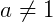 , b > 0,
, b > 0, 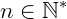 , então:
, então:
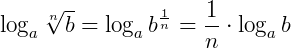
Exemplo: 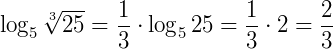
Definição de Cologaritmo
Chamamos de cologaritmo de um número b na base a, o oposto do logaritmo de b na base a. Assim, se 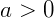 ,
, 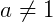 e
e 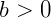 , então:
, então:
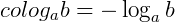
Podemos fazer a seguinte expansão:
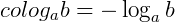
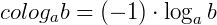
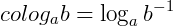
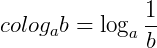
Assim, o cologaritmo de um número é o logaritmo do seu inverso, na mesma base.
Exemplos:
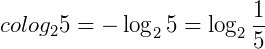
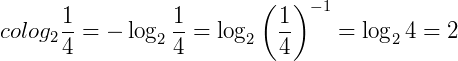
Exercícios
1) Calcule o 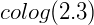
Lembrando que quando omitimos o valor da base, estamos trabalhando com a base decimal (10).
Resolvendo:
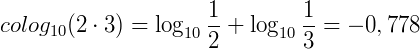
2) Calcule o 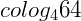
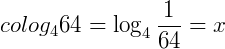
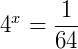
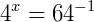
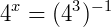
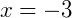
3) Calcule o 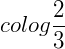
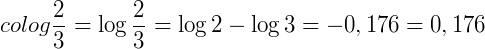
(quando resolvemos desse modo basta lembrar de trocar o sinal do resultado)
Referência:
DOLCE, Osvaldo; IEZZI, Gelson; MURAKAMI, Carlos. Fundamentos de Matemática Elementar. Logaritmos. Vol. 2. São Paulo: Atual, 1997.
Texto originalmente publicado em https://www.infoescola.com/matematica/cologaritmo/