A Equação de Bernoulli é um princípio presente na Hidrodinâmica que pode ser entendido de maneira análoga ao princípio de Stevin da Hidrostática. Isso quer dizer que como os fluidos estão em movimento, deve-se considerar um termo adicional, que não é considerado no princípio de Stevin, contendo as velocidades dos fluidos envolvidos.
Considera-se dois pontos quaisquer e dentro de um fluido em movimento sob a ação da aceleração da gravidade (situação representada pela Figura 1). Uma vez que a velocidade é uma grandeza vetorial, que sempre é tangente a trajetória, as velocidades vetoriais de e serão diferentes. O princípio de Bernoulli diz então que, deve-se levar em conta um setor potencial, um setor cinético e um setor potencial gravitacional,
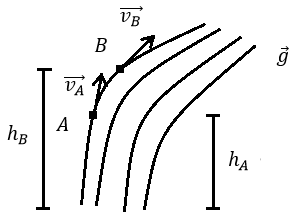
Velocidade dos pontos A e B em um fluido em movimento.
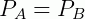
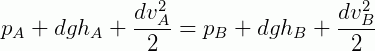
Esta equação pode ser reescrita da seguinte maneira (a Equação de Bernolli):
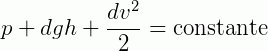
Onde p, h e v são as diferenças entre as pressões A e B, alturas A e B e velocidades A e B respectivamente.
O princípio de Bernoulli é um tipo de equação de conservação de energia e apresenta inúmeras aplicações em Mecânica dos Fluidos.
Referências:
BONJORNO, José Roberto; BONJORNO, Regina Azenha; BONJORNO, Valter; CLINTON, Márcico Ramos. Física História & Cotidiano. São Paulo: Editora FTD, 2004, volume único.
HEWITT, Paul G. Física Conceitual. Porto Alegre: Editora: Bookman, 2011, 11ª. ed. v. único.
Texto originalmente publicado em https://www.infoescola.com/fisica/equacao-de-bernoulli/