Poliedros

Na geometria espacial, as formas tridimensionais são chamadas sólidos geométricos.

Alguns exemplos:

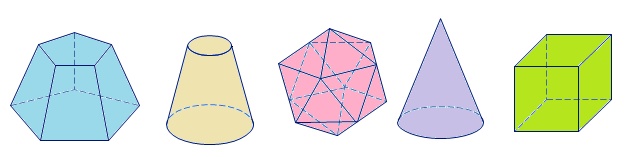
Podemos dividir os sólidos geométricos mais simples em dois tipos:

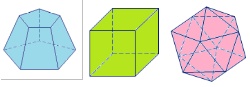
Poliedros

São aqueles cujas superfícies são formadas apenas por polígonos planos.

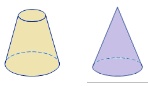
Corpos redondos

São aqueles cujas superfícies têm ao menos uma parte que é arredondada (não plana).

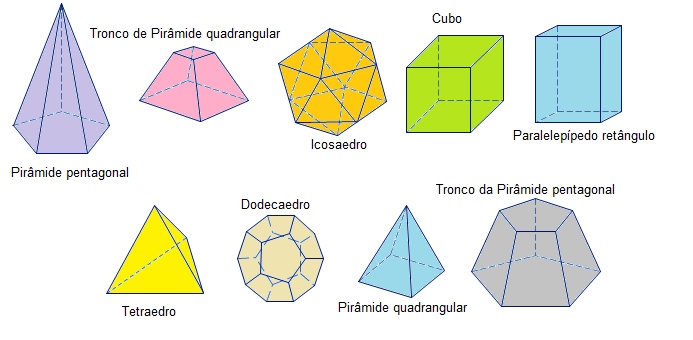
Resumindo, poliedro é um sólido geométrico que possui apenas faces planas.

Exemplos e seus nomes:

Elementos de um poliedro: vértice, face e aresta.

• Vértices: pontas.
• Faces: polígonos planos.
• Arestas: quinas.

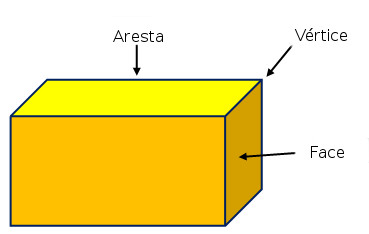
A palavra poliedro vem do grego antigo, poli significa várias e edros significa faces.

Classificação dos poliedros

Poliedros podem ser classificados em convexos e côncavos:

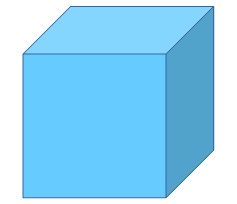
Convexo: um poliedro é convexo se qualquer segmento com extremidades dentro do poliedro estiver totalmente contido no poliedro.

Exemplo: O cubo é um poliedro convexo.

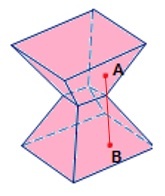
Côncavo: um poliedro é côncavo se algum segmento com extremidades dentro do poliedro possuir pontos fora do poliedro.

Exemplo: o poliedro abaixo é côncavo, pois o segmento com extremidades A e B tem pontos fora do poliedro.

Relação de Euler

Se, em um poliedro convexo, V é o número de vértices, F é o número de faces e A é o número de arestas, então vale a relação:

Observação: todo poliedro convexo obedece à relação de Euler, já os poliedros côncavos podem obedecê-la ou não.

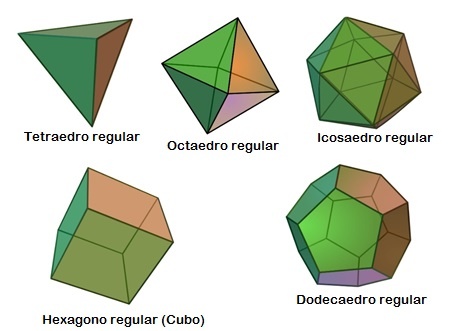
Poliedros regulares

Um polígono regular é aquele em que todos os seus lados possuem a mesma medida e todos os ângulos internos são congruentes entre si.

Considerando tal definição, observe a definição de poliedro regular. Um poliedro é chamado regular se, e somente se:

• É convexo.
• Todas as suas faces são formadas por polígonos regulares e congruentes entre si.
• Todos os vértices formam ângulos congruentes.

Existem 5, e somente 5, tipos de poliedros regulares. São eles:

Texto originalmente publicado em https://www.infoescola.com/geometria-espacial/poliedros/