Função modular

Vamos relembrar o conceito de módulo (ou valor absoluto) de um número real:

O módulo de um número real r é representado por |r| onde:

|r| = r se r ≥ 0

|r| = -r se r < 0

E também, algumas propriedades envolvendo os módulos de números reais, algumas delas são:

$|x| \geq 0 \quad \forall x \in \mathbb{R}$

$|x| = 0 \Rightarrow x = 0$

$|x| \geq x \quad \forall x \in \mathbb{R}$

$|x| \geq |-x| \quad \forall x \in \mathbb{R}$

$|x^2| = |x|^2 = x^2$

$|x+y| \leq |x| + |y|$

$|x-y| \geq |x| - |y|$

$|x \cdot y| = |x| \cdot |y|$

$|\frac{x}{y}|= \frac{|x|}{|y|}$

$||x| - |y|| \leq |x - y|$

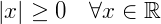
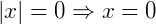
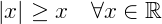
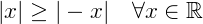
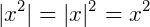
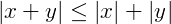
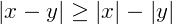
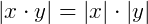
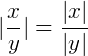
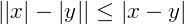
Função modular

Agora, definimos uma função modular como:

Seja uma função 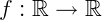$f : \mathbb{R} \rightarrow \mathbb{R}$ e dada por f(x) = |x| então:

$f(x) = \begin{cases}x,&\text{ se } x \geq 0\\-x,&\text{ se } x < 0\end{cases}$

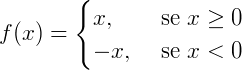
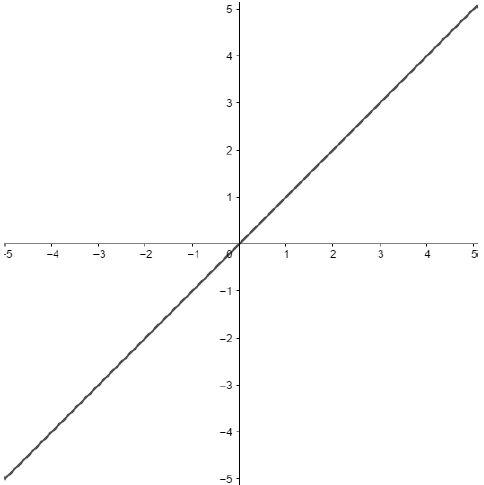
Uma alusão interessante para as funções modulares é que podemos imaginar que o eixo x é um espelho para o gráfico das funções. Tudo que está abaixo da origem do plano cartesiano no eixo y, ou seja, valores negativos de y, não assumirá valores. Vejamos abaixo o exemplo de duas funções:

f(x) = x

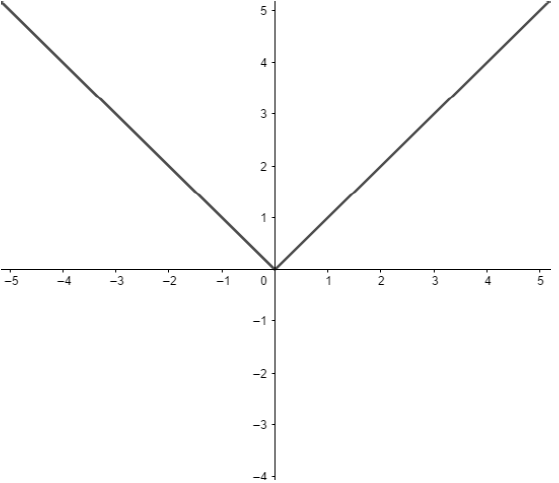
f(x) = |x|

Exemplo 1) Seja a função 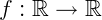$f: \mathbb{R} \rightarrow \mathbb{R}$ definida por 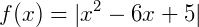$f(x) = |x^2 - 6x + 5|$, o seu gráfico é dado por:

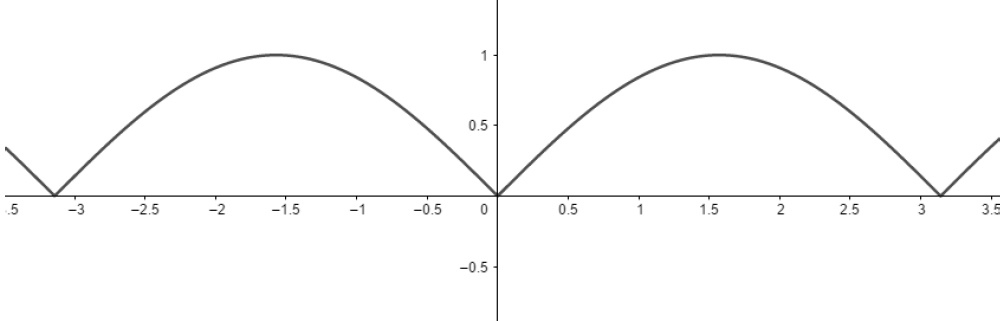
Exemplo 2) Seja a função 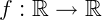$f:\mathbb{R} \rightarrow \mathbb{R}$ definida por 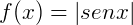$f(x) = |sen x|$, o seu gráfico é dado por:

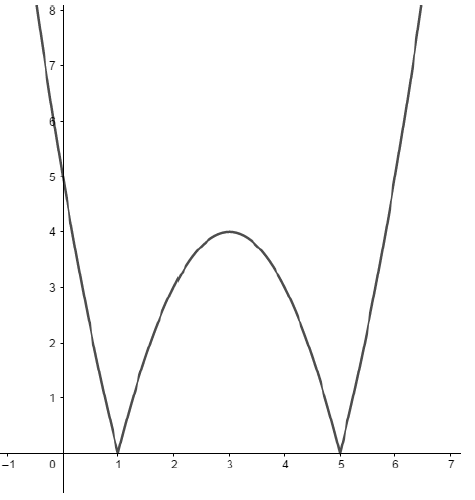
Exemplo 3) Agora a função 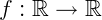$f: \mathbb{R} \rightarrow \mathbb{R}$ definida por 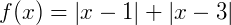$f(x) = |x-1| + |x-3|$. Para construir este gráfico devemos considerar primeiro a solução da equação modular na qual ela é definida. Para isso é necessário atribuir algumas condições eliminando os módulos das funções segundo as propriedades apresentadas. Veja abaixo:

1) Se 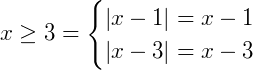$x \geq 3 = \begin{cases}|x-1| = x-1\\|x-3| = x-3\end{cases}$

Então podemos dizer que:

f(x) = (x-1) + (x-3) = x-1 + x - 3 = 2x-4

2) Se 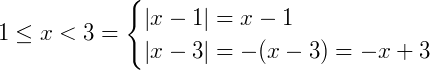$1 \leq x < 3 = \begin{cases}|x-1| = x-1\\|x-3| = -(x-3) = -x+3\end{cases}$

Logo:

f(x) = (x-1) + (-x+3) = x-1-x+3 = 2

3) Se 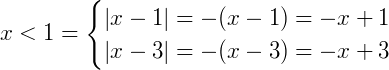$x < 1 = \begin{cases}|x-1| = -(x-1) = -x+1\\|x-3| = -(x-3) = -x+3\end{cases}$

Então:

f(x) = (-x+1) + (-x+3) = -x+1-x+3 = -2x+4

4) Concluindo que a nossa função terá como condições:

$f(x) = \begin{cases}2x-4,&\quad \text{ se } x \geq 3\\2,&\quad \text{ se } 1 \leq x < 3\\-2x+4,&\quad \text{ se } x < 1\end{cases}$

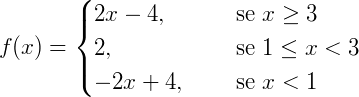
O seu gráfico então será dado por:

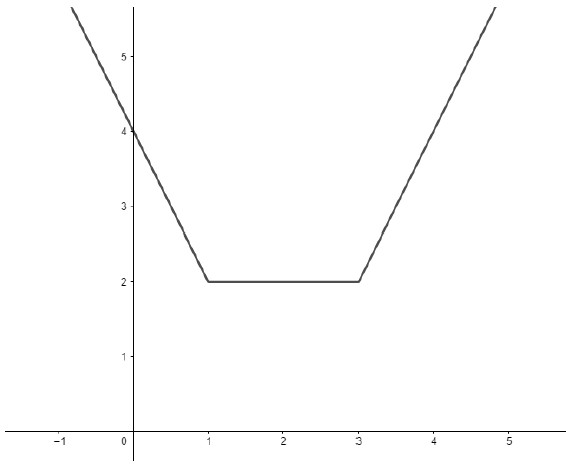
Exemplo 4) Vamos determinar o gráfico de 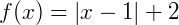$f(x) = |x-1| + 2$. Eliminando os módulos segundo as propriedades, temos que:

$f(x) = \begin{cases}x+1,&\quad \text{ se } x \geq 1\\-x+3,&\quad \text{ se } x < 1\end{cases}$

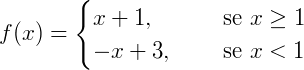
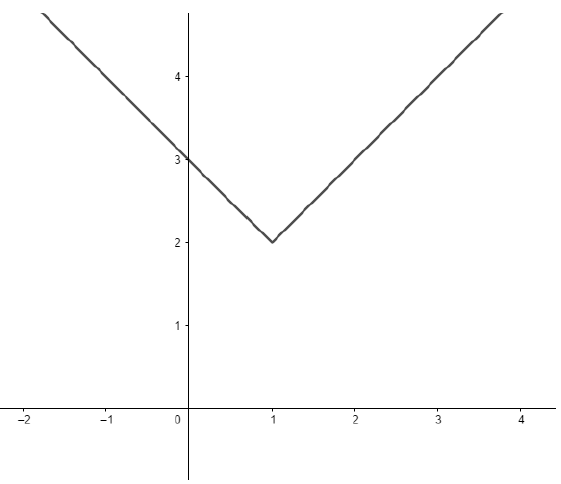
O seu gráfico será dado por:

Referências Bibliográficas:

LIMA, Elon Lages. Um Curso de Análise: Volume 1. Rio de Janeiro: IMPA, 2017.

GUIDORIZZI, Hamilton L. Um Curso de Cálculo: Volume 1. Rio de Janeiro: Editora LTC, 2001.

Texto originalmente publicado em https://www.infoescola.com/matematica/funcao-modular/