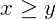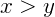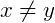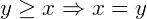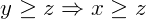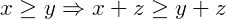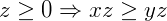Antes de introduzirmos o conceito de módulo, vamos rapidamente revisar algumas definições importantes sobre os números reais:
O conjunto dos números racionais mais os irracionais formam o conjunto dos números reais.
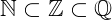
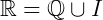
Podemos também representar o conjunto dos reais numa reta graduada:

Abaixo as desigualdades e relações de ordem de números Reais:
- Se
 , dizemos que x é maior ou igual a y;
, dizemos que x é maior ou igual a y; - Se
 , então x é maior do que y;
, então x é maior do que y; - Se
 , dizemos que x é diferente de y.
, dizemos que x é diferente de y.
Agora, algumas propriedades a respeito das desigualdades:
- Reflexiva:

- Antissimétrica:
 e
e 
- Transitiva:
 e
e 
- Compatibilidade com a Adição:

- Compatibilidade com a Multiplicação:
 e
e 
Exemplo 1) Tomemos agora 𝑥, 𝑦, 𝑧 e 𝑤, quaisquer números Reais e vamos descobrir se há uma relação de ordem entre eles dados 𝑥 ≤ 𝑦 e 𝑧 ≤ 𝑤.
Pela compatibilidade com a adição podemos dizer que:
𝑥 ≤ 𝑦 ⇒ 𝑥 + 𝑧 ≤ 𝑦 + 𝑧
𝑧 ≤ 𝑤 ⇒ 𝑦 + 𝑧 ≤ 𝑦 + 𝑤
Agora, pela propriedade transitiva temos:
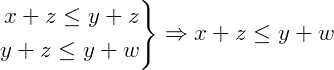
Concluindo:
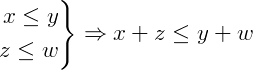
Tendo em vista a importância de relembrar essas definições, tanto dos números reais quanto das desigualdades, a definição de módulo se torna então mais clara.
O módulo de um número real 𝑟 é, que é representado por |𝑟| onde:
|𝑟| = 𝑟 se 𝑟 ≥ 0
|𝑟| = −𝑟 se 𝑟 < 0
Podemos também dizer que o módulo de um número real é a “distancia”desse número até o zero da reta real. Por exemplo, a distância do número 4 até o zero seria o seu próprio valor:
|4| = 4
Já a distância do -13 até o zero seria de apenas 13.
|−13| = 13
E também temos algumas propriedades envolvendo os módulos de números reais que valem a pena ser apresentadas. Algumas delas são:
|𝑥| ≥ 0 ∀𝑥 ∈ ℝ
|𝑥| = 0 ⇒ 𝑥 = 0
|𝑥| ≥ 𝑥 ∀𝑥 ∈ ℝ
|𝑥| ≥ |−𝑥| ∀𝑥 ∈ ℝ
|𝑥²| = |𝑥|2 = 𝑥²
|𝑥 + 𝑦| ≤ |𝑥| + |𝑦|
|𝑥 − 𝑦| ≥ |𝑥| − |𝑦|
|𝑥. 𝑦| = |𝑥|. |𝑦|
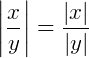
||𝑥| − |𝑦|| ≤ |𝑥 − 𝑦|
Estas propriedades e definições se tornam mais usuais quando lidamos com funções e/ou equações modulares.
Referências Bibliográficas
DEMANDA, Franklin D; WAITS, Bert K.; FOLEY, Gregory D.; KENNEDY, Daniel. Pré Calculo. São Paulo: Pearson, 2013.
GUIDORIZZI, Hamilton L. Um Curso de Cálculo: Volume 1. Rio de Janeiro: Editora LTC, 2001.
Texto originalmente publicado em https://www.infoescola.com/matematica/modulo/