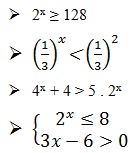O avanço comercial do século XVII fez surgirem o cálculo exponencial e os logaritmos. A partir daí, durante os três séculos que se seguiram, essas ferramentas foram utilizadas como meios sofisticados de resolução de cálculos. À medida que os estudos nesses campos foram evoluindo, os cálculos exponenciais e logarítmicos foram se tornando decisivos para a evolução da matemática e, consequentemente, das várias outras ciências que dela dependem.
Inequações exponenciais
Assim como as equações exponenciais, as inequações exponenciais são aquelas que apresentam a incógnita no expoente. Confira alguns exemplos:
Resolução de inequações exponenciais
A resolução de uma inequação exponencial poderá ser dada através das propriedades da potenciação. Mas lembre-se de que f(x) = ax somente é crescente quanto a > 1. Caso 0 < a < 1, f(x) = ax é decrescente.
Antes de resolver uma inequação exponencial, deve-se observar a situação das bases nos dois membros, caso as bases sejam diferentes, reduza-as a uma mesma base e, em seguida, forme uma inequação com os expoentes. Atente-se as regras dos sinais:
- Caso a > 1, mantenha o sinal original.
- Caso 0 < a < 1, inverta o sinal.
Essas regras serão mais bem visualizadas nas resoluções que se seguem. Vamos resolver os exemplos das inequações anteriores.
2x ≥ 128
Por fatoração, 128 = 27. Portanto:
2x ≥ 27 → como as bases são iguais e a > 1, basta formar uma inequação com os expoentes.
x ≥ 7
S = {x ∈ R | x ≥ 7}
Neste exemplo as bases já são iguais. Porém, é necessário observar que 0 < a < 1. Diante dessa condição, inverte-se o sinal.
x > 2.
S = {x ∈ R | x > 2}
4x + 4 > 5 . 2x
Perceba que, por fatoração, 4x = 22x e 22x é o mesmo que (2x)². Reescrevendo a inequação, temos:
(2x)² + 4 > 5 . 2x
Chamando 2x de t, para facilitar a resolução, ficamos com:
t2 + 4 > 5t
t2 – 5t + 4 > 0
Aqui temos uma inequação de 2º grau, onde deve ser feito o estudo dos sinais. Não vamos mostrar o processo de resolução da inequação de 2º grau, visto que o texto trata das exponenciais. Fica como sugestão de exercícios para os leitores.
Ao resolver, você encontrará D = 9, t1 = 1 e t2 = 4. Como a > 0, a concavidade da parábola ficará para cima. Isso significa que, como estamos procurando valores que tornem a inequação positiva, ficamos com:
t < 1 ou t > 4.
Retornando à variável inicial:
t = 2x
2x < 1 → x < 0 → lembre-se que todo número elevado a 1 é igual ao próprio número, e que todo número elevado a zero é igual a 1.
2x > 4 → 2x > 22 → x > 2.
S = {x ∈ R | x < 0 ou x > 2}
2x ≤ 8 → 2x ≤ 23 → x ≤ 3 (S1)
3x – 6 > 0 → 3x > 6 → x > 2 (S2)
A solução final é dada pela interseção das duas soluções encontradas.
S = S1 ∩ S2
S = {x ∈ R | 2 < x ≤ 3}
“Certo de que a vitória é a recompensa, vou lutando bravamente”.
(Robison Sá)
Referências bibliográficas:
YOUSSEF, Antonio Nicolau (et al.). Matemática: ensino médio, volume único. – São Paulo: Scipione, 2005.
IEZZI, Gelson (et al.). Matemática: ciência e aplicações, 1: ensino médio. – 6. ed. – São Paulo: Saraiva, 2010.
Texto originalmente publicado em https://www.infoescola.com/matematica/inequacao-exponencial/