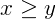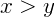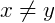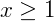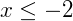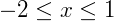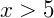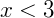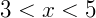Quando estudamos equações do 2º grau lidamos com igualdades, ou seja, expressões em que precisamos encontrar as raízes da equação em questão. Porém, quando tratamos de uma inequação a nossa expressão conterá, ao invés do sinal de igual (=), outros sinais que determinarão uma relação de ordem entre os seus elementos.
- Se
 , dizemos que x é maior ou igual a y;
, dizemos que x é maior ou igual a y; - Se
 , então x é maior do que y;
, então x é maior do que y; - Se
 , dizemos que x é diferente de y.
, dizemos que x é diferente de y.
Resolvendo inequações do segundo grau
Para resolver uma inequação do 2º grau, é interessante primeiro resolver a equação normalmente e depois determinar as condições de existência em função de suas raízes e de sua desigualdade. Veja abaixo alguns exemplos:
Exemplo 1) Vamos resolver a equação dada por 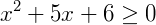 .
.
Se igualássemos a equação a zero e resolvê-la como uma equação comum do segundo grau obteríamos as raízes:
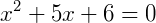
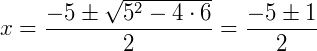
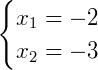
Agora devemos analisar ambas as raízes segundo a condição da equação dada onde a solução da equação deve ser maior ou igual a zero. Então devemos estudar o sinal de ambas as raízes obtidas separadamente e depois analisar a representação de ambas na reta, ou seja:
Se x for maior ou igual a -2, os valores da equação são maiores ou iguais a 0, o que cabe, analisando esta raiz a representação no intervalo:
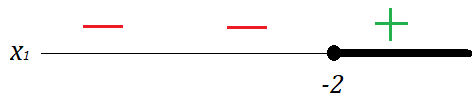
Se x for menor ou igual a -3 então os valores de x também serão maiores que zero:
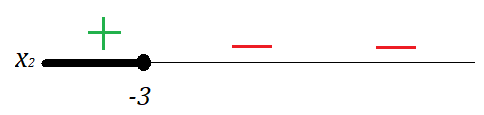
Sendo assim, o conjunto solução de nossa inequação será representado na reta como:
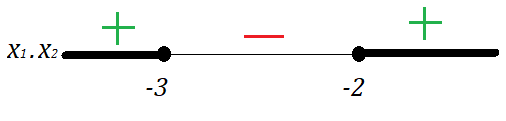
Ou pode ser escrito como:
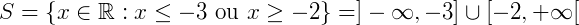
Exemplo 2) Agora, vamos analisar a equação dada por 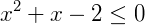 .
.
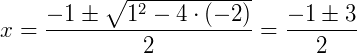
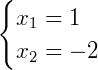
Analisando o sinal repetindo o mesmo procedimento acima, obtemos:
- Se
 , os valores da equação serão maiores ou igual zero.
, os valores da equação serão maiores ou igual zero. - Se
 , os valores também serão maiores ou iguais a zero.
, os valores também serão maiores ou iguais a zero. - Se
 , então os valores serão menores do que zero, o que satisfaz a nossa condição de existência da equação. Logo:
, então os valores serão menores do que zero, o que satisfaz a nossa condição de existência da equação. Logo:

E sua solução pode ser escrita como:
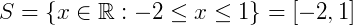
Exemplo 3) Estudemos a equação 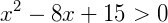 .
.
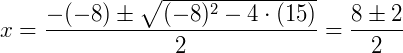
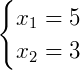
- Se
 , os valores da equação serão maiores do que zero.
, os valores da equação serão maiores do que zero. - Se
 , os valores também serão maiores do que zero.
, os valores também serão maiores do que zero. - Se
 , então os valores serão menores do que zero. Então podemos afirmar que:
, então os valores serão menores do que zero. Então podemos afirmar que:

E o conjunto solução será:
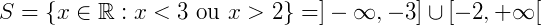
Texto originalmente publicado em https://www.infoescola.com/matematica/inequacao-do-segundo-grau/