Números Inteiros

No conjunto dos números naturais temos:

$\mathbb{N} = \{0, 1, 2, 3, 4, 5, 6, ... \}$

Como as representações (2) e (+2) têm o mesmo significado, o conjunto dos números naturais também pode ser escrito desta forma:

$\mathbb{N} = \{0, +1, +2, +3, +4, +5, +6, ... \}$

Dizemos que os números naturais correspondem aos inteiros positivos, com o zero.

Observe agora o conjunto dos números inteiros negativos:

{..., -6, -5, -4, -3, -2, -1}

Reunindo os números naturais com os inteiros negativos, obtemos o conjunto dos números inteiros, que é representado como:

$\mathbb{Z}=\{..., -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, ...\}$

ou assim:

$\mathbb{Z}=\{..., -5, -4, -3, -2, -1, 0, +1, +2, +3, +4, +5, ...\}$

Considere a reta r abaixo. Para representar os números negativos e os números positivos sobre ela, começaremos com a escolha de um ponto que será a origem. Vamos escolher o ponto O. A partir da origem O, marcamos os outros pontos, adotando uma mesma unidade de comprimento.

O ponto A está no sentido positivo, a 3 unidades de O: corresponde ao número positivo 3 ou +3.

O ponto C está no sentido negativo, a 1 unidades de O: corresponde ao número negativo -1.

Dizemos que o ponto A tem abscissa +3 e o ponto C tem abscissa -1.

Módulo ou valor absoluto de um número inteiro

Observe esta reta numerada:

A distância do ponto A (representado por +3) à origem é de 3 unidades.

O número 3, que expressa a distância de A à origem O, é chamado de módulo ou valor absoluto do número inteiro +3. Indicamos assim: |+3| = 3.

Observe que a distância do ponto B (representado por -3) à origem também é de 3 unidades, ou seja, o módulo ou o valor absoluto de -3 também é 3. Simbolicamente: |+3| = 3.

Chamamos de módulo ou valor absoluto de um número inteiro a distância do ponto que representa esse número até a origem.

Outros exemplos:

• O valor absoluto de -3 é 3, ou seja, |-3| = 3.
• O módulo de +9 é 9, ou seja, |+9| = 9.
• O módulo de 0 é 0, ou seja, |0| = 0.
• O valor absoluto de -20 é 20, ou seja, |-20| = 20.

O módulo de um número diferente de zero é sempre positivo.

Números opostos ou simétricos

Vamos considerar em uma reta numerada o ponto O, correspondente ao número zero, como origem. Temos, nesse caso, um exemplo de simetria central, ou seja, uma simetria em relação a um ponto O.

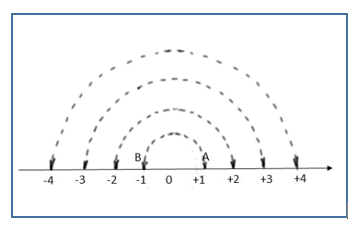
Os pontos A e B estão à mesma distância de O. Dizemos que +1 e -1 são números opostos ou simétricos. Veja mais alguns exemplos de números opostos: +2 e -2, +3 e -3, e assim por diante.

Veja como indicamos o oposto ou simétrico de um número:

• O oposto de 4 → -4
• O simétrico de +7 → -(+7) = -7
• O oposto de -9 → +9 ou 9.
• O simétrico de zero é o próprio zero.
• O oposto de -7 → -(-7) = +7 ou 7.
• O oposto de +35 → -(+35) = -35.

Comparação de números inteiros

Comparar dois números significa dizer se o primeiro é maior do que (>), menor do que (<) o igual ao (=) segundo número.

1º caso: Para comparar dois inteiros positivos, basta pensar em dois números naturais, ou seja, o maior deles é o que tem o módulo maior.

Exemplos: +245 > + 186 ; +96 < +102

2º caso: Para comparar um número inteiro positivo com o zero, o maior deles é sempre o número positivo.

Exemplos: +53 > 0 ; 0 < +38

3º caso: Quando comparamos um número inteiro negativo com o zero, o maior deles é sempre o zero.

Exemplos: - 25 < 0 ; 0 > -18

4º caso: Quando comparamos um número positivo com um número inteiro negativo, o maior deles é sempre o número positivo.

Exemplos: +25 > -19 ; -64 < +18

5º caso: Quando comparamos dois números negativos, o o maior deles é o que tem menor módulo.

Exemplos: -34 < -19 ; -6 > -12 ; -9 > -15

Explorando a ideia de números negativos

Podemos identificar em várias situações do cotidiano a aplicação dos número inteiros. Vejam alguns exemplos:

Temperatura

A unidade de medida de temperatura mais utilizada no Brasil é o grau Celsius (^o C).

As medidas de temperatura maiores do que 0^o C são as medidas acima de zero. Dizemos que elas têm valor positivo: +3 ^o C, +15 ^o C, +18 ^o C, + 26 ^o C, etc.

As medidas de temperatura menores do que 0^o C são as medidas abaixo de zero. Dizemos que elas têm valor negativo: -4^o C; -10^o C; -12^o C, etc.

Altitude

Para identificar a altitude de um lugar também usamos números positivos e números negativos. Altitudes acima do nível do mar são indicadas por números positivos. Altitudes abaixo do nível do mar são indicadas por números negativos. Para o nível do mar, usamos o zero.

Por exemplo, o ponto mais alto da superfície terrestre é o monte Everest, na fronteira entre a China e o Nepal, com altitude aproximada de 8848 metros acima do nível do mar (ou +8848 m). E o ponto mais baixo é a fossa das Marianas, localizada no oceano Pacífico, a leste das Filipinas. Sua altitude é de 11034 metros abaixo do nível do mar (-11034 m).

Texto originalmente publicado em https://www.infoescola.com/matematica/numeros-inteiros/