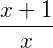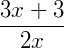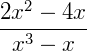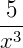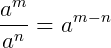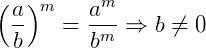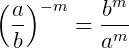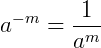Frações algébricas são todas as frações em que variáveis aparecem no denominador ou no numerador da mesma. Elas podem aparecem em um problema onde devemos encontrar os valores dessas variáveis ou apenas para simplificar uma expressão. Vamos dar alguns exemplos do que seriam frações algébricas:
É importante lembrar que, uma fração é um número escrito na forma:
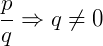
A potenciação de frações algébricas é bem similar a potencia de uma fração comum. Vamos rever algumas propriedades de potenciação envolvendo frações. Abaixo, 𝑎 e 𝑏 são bases, 𝑚 e 𝑛 são expoentes:
Note que até os exemplos acima, criados especificamente como uma forma geral para operações de potências de frações, são representados como frações algébricas onde as variáveis são 𝑎 e 𝑏 , e os expoentes são constantes. Vamos agora trabalhar com potências, porém envolvendo frações algébricas:
Exemplo 1) Vamos utilizar a propriedade 2 para calcular esta potência: 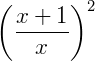
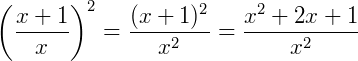
Exemplo 2) Aqui, basta utilizar a propriedade 3 para calcular: 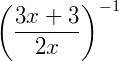
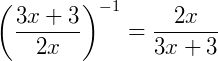
Exemplo 3) Simplifique a fração algébrica abaixo, sendo (𝑥𝑦) ≠ 0. Neste exemplo cada termo está elevado a uma potência individualmente:
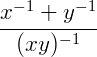
Então:
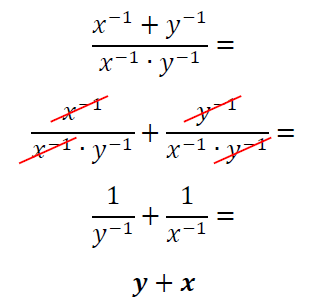
Exemplo 4) Agora um mais simples. Calcule 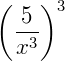 .
.
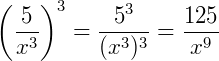
Leia também:
Referências Bibliográficas:
GONÇALVES, Adilson. Introdução à Álgebra. Rio de Janeiro: IMPA, 1999.
MORGADO, A. C.; WAGNER, E.; JORGE, M. Álgebra I. São Paulo: Livraria Francisco AlvesEditora S.A., 1974.
Texto originalmente publicado em https://www.infoescola.com/matematica/potenciacao-de-fracoes-algebricas/