A potenciação é uma notação simplificada de representar a multiplicação um número, que chamamos de base, repetidamente pelo valor de uma potência que nos determina quantas vezes devemos multiplicar este número. De uma forma prática, dado um número , elevado a potência de expoente n:
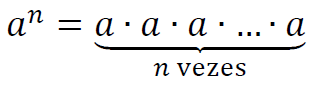
Exemplos:
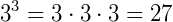
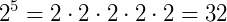
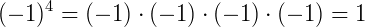
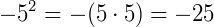
Vale a pena lembrar que quando uma base está elevada a potência 2, dizemos que ela está elevada ao quadrado. Quando a potência é 3, dizemos que está elevada ao cubo. Existem algumas observações interessantes á respeito de potências, essas são:
⇒ Toda potência de 0 com expoentes positivos é igual a 0. Exemplo: 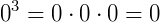
⇒ Não se definem 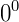 nem
nem 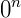 com n como um número negativo, ou seja, são valores indeterminados.
com n como um número negativo, ou seja, são valores indeterminados.
⇒ Toda potência de expoente 0 é igual a 1.
Sendo assim, vamos apresentar agora algumas regras de potenciação muito úteis. Abaixo, e são bases, e são expoentes:
1. 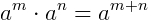
2. 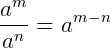
3. 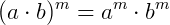
4. 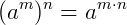
5. 
6. 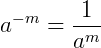
7. 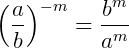
8. 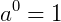
9. 
10. 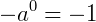
Exemplos:
Agora iremos calcular algumas expressões utilizando algumas propriedades acima. Abaixo, o passo-a-passo das operações necessárias, lembrando que, é interessante observar as propriedades à medida que a conta é desenvolvida, garantindo assim um melhor entendimento.
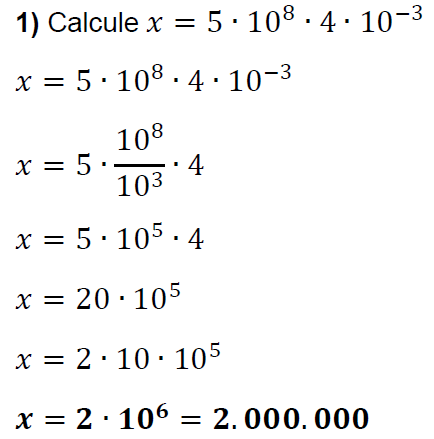
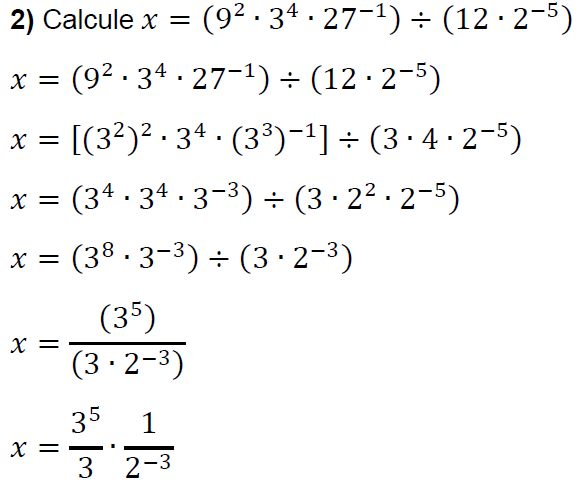


Note que em todos os exemplos acima, utilizamos pelo menos uma propriedade mostrada.
Leia também:
Referências Bibliográficas
MORGADO, A. C.; WAGNER, E.; JORGE, M. Álgebra I. São Paulo: Livraria Francisco Alves Editora S.A., 1974.
HEFEZ, Abramo. Elementos da Aritmética. Rio de Janeiro: SBM, 2011.
Texto originalmente publicado em https://www.infoescola.com/matematica/potencias/