Progressões geométricas

Assim como em uma progressão aritmética, a Progressão Geométrica (P.G) também é representada por uma sequência, porém seus elementos são dados pelo produto do termo anterior por uma constante que chamaremos de razão q. Em outras palavras, dada a sequência:

(a₁, a₂, a₃, a₄, ..., a_n)

Temos que:

a₂ = a₁ . q

a₃ = a₂ . q = (a₁ . q) . q = a₁ . q²

a₄ = a₃ . q = (a₂ . q) . q = [(a₁ . q) . q ] . q = a₁ . q³

...

Naturalmente, se quisermos obter a razão de uma P.G., devemos dividir um termo a_n pelo seu anterior, assim:

$q=\frac{a_2}{a_1}=\frac{a_3}{a_2}=\frac{a_4}{a_3}=...\frac{a_n}{a_{n-1}}$

Ao continuarmos a operação para determinar um termo qualquer em uma P.G., obtemos então a fórmula do termo geral:

$a_n=a_1\cdot q^{n-1}$

E supondo um caso em que não sabemos qual é o seu primeiro termo, podemos usar uma forma generalizada do termo geral da P.G. Sejam m e n posições consecutivas quaisquer dos elementos, temos:

$a_n=a_m\cdot q^{m-n}$

Interpretação geométrica da P.G.

Podemos representar o termo geral de uma P.G. como uma função do tipo f(x), onde podemos reescrever a fórmula em função de x e também desenhar o gráfico da função. Dizemos então que:

$f(x)=a_q\cdot q^x$

Supondo conhecidos os valores de a₁ e de q, a sua razão, a fórmula do termo geral assumirá então a forma de uma função exponencial. Vejamos um exemplo em que a_n = ½ e que q = 2, escrevemos:

$f(x)=\frac{1}{2}\cdot(2)^x$

Sabemos, por definição que esta P.G. será dada por:

$(\frac{1}{2}, 1, 2, 4, 8, ...)$

Neste exemplo, o nosso primeiro termo será dado por $f(0)=\frac{1}{2}$ o que claramente já foi dado, confirmando então que o zero da função é o termo a₁. Abaixo segue o gráfico da função onde estão indicados os quatro primeiros termos da P.G.:

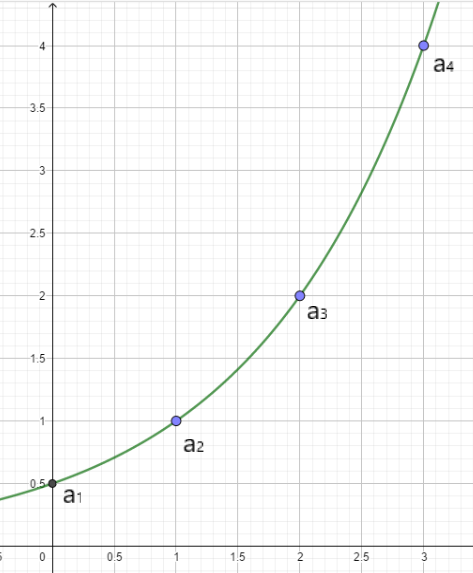
Vemos que os valores de f(1), f(2), ..., f(x) com x sendo um número inteiro serão os termos da P.G.

Tipos de progressão geométrica

Crescente

Quando a razão q >1 e os termos são positivos ou quando 0 < q < 1 e os termos são negativos. Exemplos:

(1, 4, 16, 64, ...), onde q = 4

(-150, -30, -6, ...), onde q = ½

Decrescente

Quando 0 < q < 1 e os termos são positivos, ou quando q > 1 e os termos negativos. Por exemplo:

(200, 100, 50, ...), onde q = ½

(-1, -3, -9, ...), onde q = 3

Oscilante

Quando q < 0, ou seja:

(3, -6, 12, -24, ...), onde q = -2

Soma dos termos de uma Progressão Geométrica finita

Seja uma P.G. (a₁, a₂, a₃, a₄, ..., a_n) e S_n soma dos seus termos, podemos então escrever:

$S_n=a_1+a_2+a_3+a_4+...+a_{n-1}+a_n$

Multiplicando ambos os lados da equação por q temos:

$q\cdot S_n=q\cdot(a_1+a_2+a_3+a_4+...+a_{n-1}+a_n)$

$q\cdot S_n=q\cdot a_1+q\cdot a_2+q\cdot a_3+q\cdot a_4+...+q\cdot a_{n-1}+q\cdot a_n)$

E que pela definição:

$q\cdot S_n=a_2+a_3+a_4+...+a_n+q\cdot a_n$

Podemos então dizer que:

$S_n-q\cdot S_n=(a_1+a_2+a_3+...+a_{n-1}+a_n)-(a_2+a_3+...+a_n+q\cdot a_n)$

O que nos resulta em:

$S_n-q\cdot S_n=a_1-q\cdot a_n$

E pela equação do termo geral, $a_n=a_1\cdot q^{n-1}$ podemos:

$S_n-q\cdot S_n=a_1-q\cdot(a_1\cdot q^{n-1})$

Isolando as variáveis:

$S_n(1-q)=a_1(1-q^n)$

Por fim, obtemos então a fórmula da soma da P.G. finita:

$S_n=a_1\cdot\frac{(1-q^n)}{(1-q)}$

OBS: Se a razão for igual a um (q=1), em outras palavras, se a P.G. for constante (onde todos os seus termos são iguais) então não será possível obter a soma dos seus termos.

Referências Bibliográficas:

DANTE, Luiz Roberto. Matemática: Contextos & Aplicações - Volume 1. São Paulo: Editora Ática, 2011.

IEZZI, Gelson. Fundamentos de Matemática Elementar – Volume 4: São Paulo: Editora Atual, 2013.

Texto originalmente publicado em https://www.infoescola.com/matematica/progressoes-geometricas/