Da experiência cotidiana, sabe-se que qualquer objeto lançado para cima a partir da superfície terrestre tende a retornar à superfície. Nota-se isso no lançamento de uma pedra, nos jatos d’água expelidos por uma fonte ou no arremesso de uma bola de basquetebol rumo à cesta. Esse retorno dos objetos ao solo após o lançamento ocorre em virtude da atração gravitacional entre a Terra e o objeto arremessado. Tal atração, tão familiar a nós, é o que nos mantém ligados à superfície do planeta; é o que impede que um simples salto nos projete pelo espaço afora.
É conhecido também o fato de que um objeto lançado para cima atinge maiores altitudes a cada vez que é atirado com maior velocidade. Desprezando a resistência do ar e a presença de qualquer obstáculo na atmosfera, é possível deduzir que deve haver uma certa velocidade de lançamento grande o suficiente para que o objeto se distancie do planeta Terra de tal forma que jamais retorne à sua superfície. Em uma posição tão distante, o objeto estaria livre da influência da gravidade do planeta, conseguindo escapar de seu campo gravitacional. De fato, tal velocidade existe e damos a ela o nome de velocidade de escape.
Em termos formais, a velocidade de escape é a velocidade mínima que um objeto precisa ter para se deslocar da superfície de um corpo até o infinito. Saindo da Terra, por exemplo, um projétil que fosse lançado com essa velocidade iria viajar indefinidamente, sempre com velocidade progressivamente menor, sem nunca ser parado pela força gravitacional da Terra. O valor da velocidade de escape, que permitiria ao projétil essa viagem, pode ser calculado comparando a energia inicial do projétil e à sua energia final.
Da lei da gravitação universal, sabemos que a força gravitacional entre a Terra e o projétil é proporcional ao produto de suas massas e inversamente proporcional à distância entre eles. Assim, quando chegasse a uma distância infinita, a força entre o projétil e a Terra seria zero. Como a velocidade de lançamento do projétil seria exatamente igual à velocidade de escape, podemos assumir que sua velocidade ao final da trajetória também seria zero. Do princípio de conservação da energia, esse cenário apenas seria possível se a energia cinética do projétil fosse igual à sua energia potencial gravitacional no momento do lançamento. Trabalhando essa relação em termos matemáticos, chegamos à equação abaixo:
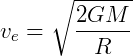
que representa a velocidade de escape ve calculada na superfície da Terra, que possui massa M e raio R, sendo G a constante gravitacional universal.
Embora a Terra tenha sido utilizada na obtenção da equação, a expressão é válida para qualquer outro corpo, com os termos M e R representando a massa e o raio do corpo em questão. Algo notável sobre essa relação é a demonstração de que a velocidade de escape não depende das características do projétil, dependendo apenas da massa e do tamanho do corpo a partir do qual ele é lançado. Quanto mais massivo ou mais compacto for um corpo, maior a velocidade de escape a partir de sua superfície. Na Terra, por exemplo, a velocidade de escape é de 11,2 km/s. Já na superfície do Sol, cuja massa é bem maior, um projétil precisaria ser lançado com a velocidade mínima de 617 km/s para escapar de sua atração gravitacional.
Referências:
CHAVES, A. Física Básica: Mecânica. v. 1. Rio de Janeiro: Reichmann & Affonso Ed., 2001. p. 175.
HEWITT, P. G. Conceptual Physics. 10. ed. San Francisco: Pearson, 2006. p. 201-204.
Texto originalmente publicado em https://www.infoescola.com/astronomia/velocidade-de-escape/