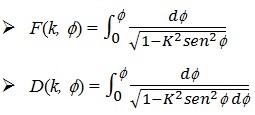A gênese de muitas descobertas matemáticas que nos beneficia até os dias atuais ocorreu num passado bastante remoto. Várias pessoas ligadas à matemática, seja pelo profissionalismo ou mesmo pela simples admiração pela ciência das formas e nos números, contribuíram para a sua evolução, dedicando seu tempo, seus esforços e doando ao mundo um pouco da sua capacidade intelectual. O conhecimento matemático evolui pela sua disseminação, pelo compartilhamento, assim como todo conhecimento.
Registros históricos
A partir do século XVII começou a surgir as primeiras ideias sobre o conceito de função, com a necessidade de observação dos fenômenos e das leis que buscavam explica-los. Galileu Galilei (1564-1642) e Isaac Newton (1642-1727), por exemplo, utilizaram em seus trabalhos algumas noções de lei e dependência, como hoje sabemos, fortemente ligadas ao conceito de função.
No século XVIII, Jean Bernoulli, matemático suíço (1667-1748) utilizou o termo função, assim designando os valores obtidos por operações entre variáveis e constantes. Ainda no século XVIII, Leonhard Euler (1707-1783) fez uso da notação atual, mas foi Gottfried Wilhelm Leibniz (1646-1716) quem criou o termo função.
Entre 1811 e 1819 o grande matemático Davies’ Legendre, publicou um tratado em três volumes denominado “Exercices du calcul integral”, rivalizando em pé de igualdade, tanto em qualidade quanto em autoridade com o tratado de Leonhard Euler. Um pouco mais adiante, Legendre expandiu o seu trabalho obtendo outros três importantes volumes e formando o “Traité des fonctions elliptiques et des intégrales eulerianas", algo entre os 1825 e 1832. Foi de Legendre que partiu o termo Equações Eulerianas para as equações Beta e Gama. Outra contribuição de Legendre são as integrais elíticas de primeira e segunda espécie:
O mais importante matemático do século XVIII foi Joseph Louis Lagrange. Dentre várias contribuições de Lagrange estão estudos sobre o cálculo de variações, à época ramo novo da matemática, cujo nome era originado de notações usadas pelo próprio Lagrange por volta de 1760. Em linguagem simples, o cálculo de variações trata de encontrar uma relação funcional (y = f(x)), de maneira que uma integral 
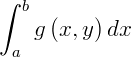seja máxima ou mínima.
Quedas mais rápidas e problemas de isoperimetria eram casos especiais do cálculo de variações. No ano de 1755 Lagrange escrevera a Euler mostrando os métodos gerais que ele tinha desenvolvido para resolução de problemas dessa natureza. Euler, por sua vez, humilde e generosamente, adiou a publicação de um trabalho semelhante para que Lagrange recebesse todo o crédito.
Ainda voltando no tempo, já clara as várias contribuições de tantas pessoas ligadas à matemática para o desenvolvimento dos conceitos sobre função, a definição antiga que talvez mais se assemelhe com a que utilizamos hoje é do matemático alemão Peter G. Lejeune Dirichlet (1805-1859), diferenciando-se da atual apenas pela não criação, à época, da Teoria dos Conjuntos.
“O futuro é determinado por ações do presente.”
(Robison Sá)
Referências bibliográficas:
BOYER, Carl B. História da matemática / Carl B. Boyer, revista por Uta C. Merzbach; tradução Elza F. Gomide – 2ª ed. – São Paulo: Edgard Blucher, 1996.
YOUSSEF, Antonio Nicolau; SOARES, Elizabeth; FERNANDEZ, Vicente Paz. – São Paulo: Scipione, 2005.
Texto originalmente publicado em https://www.infoescola.com/matematica/aspectos-historicos-sobre-funcao-matematica/