Vimos nos artigos: Equações Diferenciais e Equações Diferenciais de 1ª Ordem uma breve introdução ao estudo das EDOs. Neste trataremos um pouco mais sobre EDOs Exatas e Lineares. Se o leitor ainda não visitou os artigos acima citados, vale a pena conferir não só esses artigos, mas também o de Equações Diferenciais Separáveis.
Equações Lineares
Vamos relembrar o conceito de uma equação linear. Uma ED é chamada de linear se é possível escrevê-la na forma:
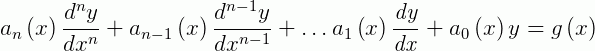
Em outros termos, podemos classificar as EDs lineares de 1ª ordem com duas propriedades:
a) A variável dependente de y e todas as suas derivadas são do primeiro grau, ou seja, n=1.
b) Cada coeficiente depende apenas da variável independente x.
Em outras palavras, uma equação diferencial de 1ª ordem da forma:
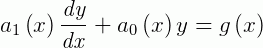
É linear.
Dividindo a equação pelo seu coeficiente 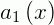 , obtemos uma forma mais útil para uma ED linear:
, obtemos uma forma mais útil para uma ED linear:
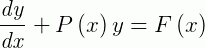
Onde devemos procurar uma solução em um intervalo I em que as funções 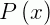 e
e 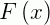 sejam contínuas.
sejam contínuas.
Fator de Integração 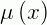
Usando diferenciais podemos escrever a equação acima como:
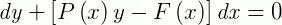
As EDOs lineares possuem uma propriedade na qual podemos sempre encontrar uma função 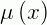 que é uma EDO exata, ou seja:
que é uma EDO exata, ou seja:
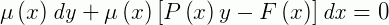
Sendo assim, se:
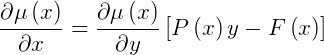
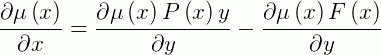
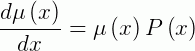
Que é uma EDO separável. Logo, a sua solução será:
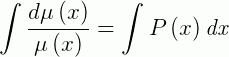
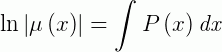
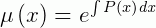
Para reduzir a nossa notação, podemos escrever a expressão acima como:
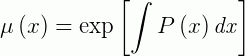
Então, a função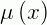 que encontramos acima é chamada de fator de integração para a EDO linear. Se substituirmos
que encontramos acima é chamada de fator de integração para a EDO linear. Se substituirmos 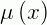 na expressão:
na expressão:
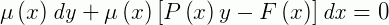
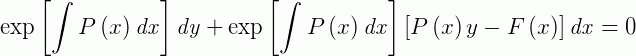
Obtemos como resultado:
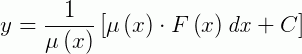
Vejamos exemplos de suas aplicações:
1 – Vamos obter uma solução para a EDO:
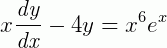
Multiplicando toda a equação por 1/x temos:
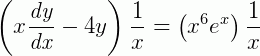
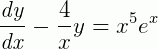
Pela definição:
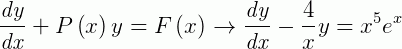
Então:
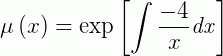
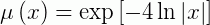
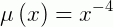
Usando:
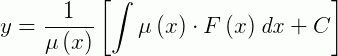
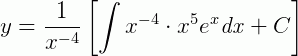
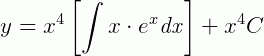
O resultado desta integral, pelo método de integração por partes, temos:
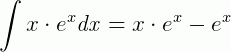
Substituindo, temos:
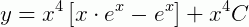
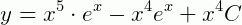
Que é o resultado de nossa EDO.
Equações Exatas
São chamadas de EDOs exatas as que podem ser escritas da forma:
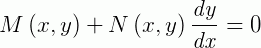
Onde as funções 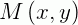 e
e 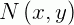 satisfazem a igualdade:
satisfazem a igualdade:
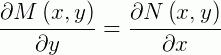
Função 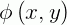
Seja um retângulo 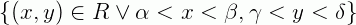 em que
em que 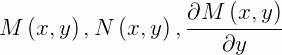 e
e 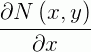 são contínuas, então existe uma função
são contínuas, então existe uma função 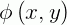 tal que:
tal que:
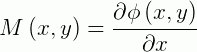
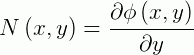
Substituindo esses valores, temos:
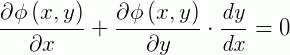
E pela regra da cadeia obtemos a relação abaixo:
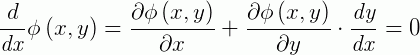
Então, a solução geral da equação será dada por:
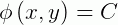
Devemos encontrar agora a própria função 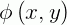 . Integrando a igualdade abaixo em relação a
. Integrando a igualdade abaixo em relação a 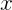 , obtemos:
, obtemos:
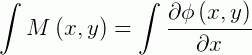
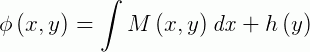
Em que 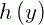 é a função
é a função 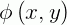 a ser determinada. Substituindo na igualdade abaixo:
a ser determinada. Substituindo na igualdade abaixo:
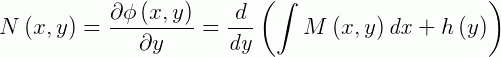
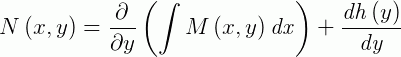
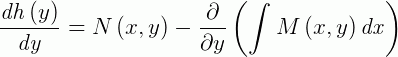
E integrando ambos os lados da igualdade, temos:
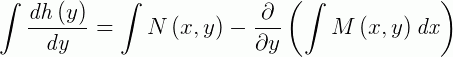
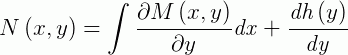
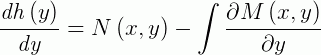
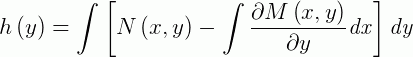
Portanto, a solução geral de uma equação exata é dada por:
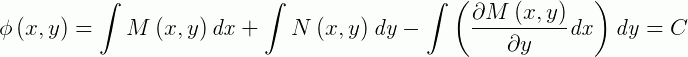
Vejamos agora uma aplicação.
2 – Vamos obter a solução da EDO abaixo:
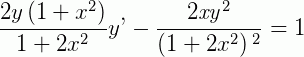
Reescrevendo temos:
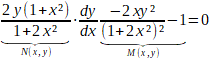
Para sabermos se a EDO é exata, devemos primeiro identificar se:
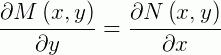
Então:
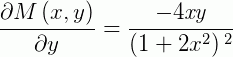
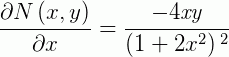
Logo, a EDO acima é exata. Continuando, devemos encontrar uma função 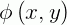 tal que:
tal que:
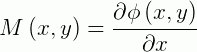
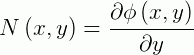
E por consequência:
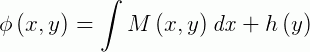
Logo:
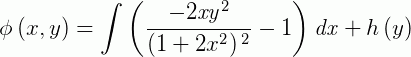
O resultado da integral é dado por:
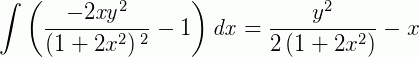
Substituindo:
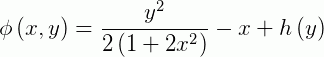
E como:
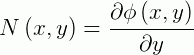
E:
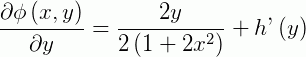
Então:
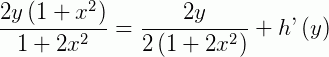
Isolando 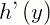 e resolvendo a expressão, temos:
e resolvendo a expressão, temos:
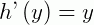
Que é uma EDO separável. Ou seja:
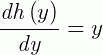
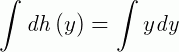
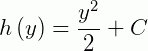
Concluindo, a solução da EDO exata será dada por:
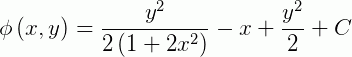
Referências bibliográficas:
ZILL, Dennis G; CULLEN, Michael R. Equações Diferenciais – Volume 1. São Paulo – Pearson Makron Books, 2001.
BASSALO, José Maria FIlardo; CATTANI, Mauro Sérgio Dorsa. Elementos de Física Matemática – Volume 1. São Paulo – Livraria da Física, 2010.
ARFKEN, George B; WEBER, Hans J; HARRIS, Frank E. Física Matemática: Métodos Matemáticos para Engenharia e Física – 7a Ed. Rio de Janeiro: Elsevier, 2017.
Texto originalmente publicado em https://www.infoescola.com/matematica/equacoes-lineares-e-exatas/