Função inversa

Antes de apresentarmos o conceito de funções inversas é necessário entendermos a definição formal de imagem direta e imagem inversa.

Considere uma função dada por f: E → F onde o conjunto E é o domínio da função e F o contradomínio:

Imagem Direta: Seja um conjunto A tal que A ⊂ E, chamamos de imagem direta de A segundo f, a função indicada por f(A) o seguinte subconjunto de F:

f(A) = {f(x) : x ∈ A}

Em outras palavras, f(A) é o conjunto das imagens de f dos elementos de A.

Imagem Inversa: É chamado imagem inversa de um conjunto B tal que B ⊂ F, segundo a função f o seguinte subconjunto de E:

f^-1(B) = {x ∈ E : f(x) ∈ B}

Dizemos então que f^-1(B) é o conjunto dos elementos de E que tem imagem em B.

Seguindo então pela definição de imagem inversa enunciamos o conceito de função inversa. Seja uma função definida como f:E → F. Dizemos que a função f admite uma inversa f^-1: F → E, se, e somente se, as composições abaixo forem verdadeiras, onde Id é a chamada Função Identidade. Desta forma:

f o f^-1 = Id_F – Quando inversa à direita

f^-1 o f = Id_E – Quando inversa à esquerda

Uma função só admite inversa à esquerda, se, e somente se, a função for Injetora, e à direita se a função for Sobrejetora. Em outras palavras, quando uma função admite uma inversa, o domínio da função f será o contradomínio da função f^-1.

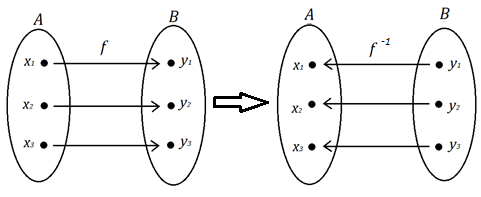
Vale lembrar que nem todas as funções admitem uma inversa, ou seja, nem todas as funções são invertíveis mesmo que o seu domínio seja um conjunto não vazio. Quando isto ocorre, dizemos que:

f^-1(x) = ∅

Obtendo a inversa de funções reais

Se tratamos de uma função definida nos reais, tal que 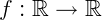$f : \mathbb{R} \rightarrow \mathbb{R}$ é uma função bijetora onde y = f(x), então para obtermos a sua inversa podemos reescrever a função da forma x = g(y) tal que x dependa de y. Com isso temos que esta nova função g(y) = f^-1.

Gráfico de funções inversas

O gráfico de uma função inversa f^-1 possui uma simetria em relação a função f. Vejamos abaixo um exemplo onde podemos notar que há uma simetria com a reta y=x entre uma função f e f^-1 e que os pontos correspondentes ao eixo de simetria y=x de ambas as funções são equidistantes:

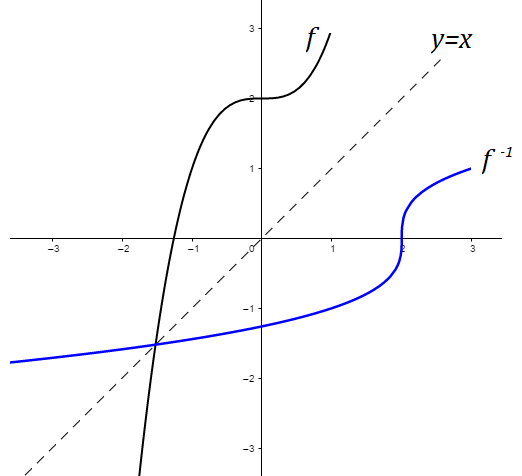
Exemplo 1) Sejam a função 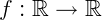$f : \mathbb{R} \rightarrow \mathbb{R}$ com f(x) = 2x+1. Para obtermos a sua inversa devemos encontrar uma função que satisfaça a condição x=g(y). Algebricamente podemos trocar a variável x pela variável y na função original, da seguinte maneira:

y = 2x+1

x = 2y+1

Agora, isolando y nesta nova expressão obteremos uma função x=g(y). Sendo assim:

x = 2y+1

2y = 1-x

$y = \frac{1-x}{2} = f^{-1}(x)$

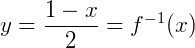
Com isso temos a função inversa. Note agora a comparação dos gráficos de f e f^-1. Percebemos que existe uma simetria entre as duas retas:

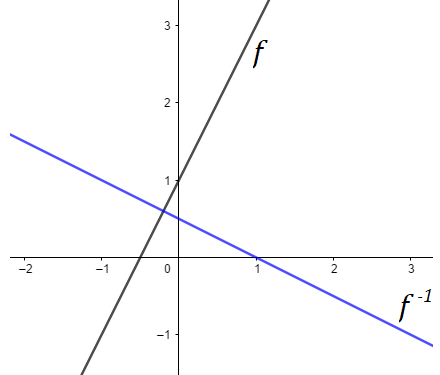
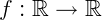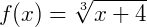Exemplo 2) Agora, seja a função $f : \mathbb{R} \rightarrow \mathbb{R}$ com $f(x) = \sqrt[3]{x+4}$. Vamos obter a sua inversa:

$y = \sqrt[3]{x+4}$

$y^3 = x+4$

$x^3 = y+4$

$y = x^3 - 4 = f^{-1}(x)$

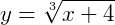
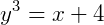
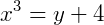
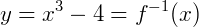
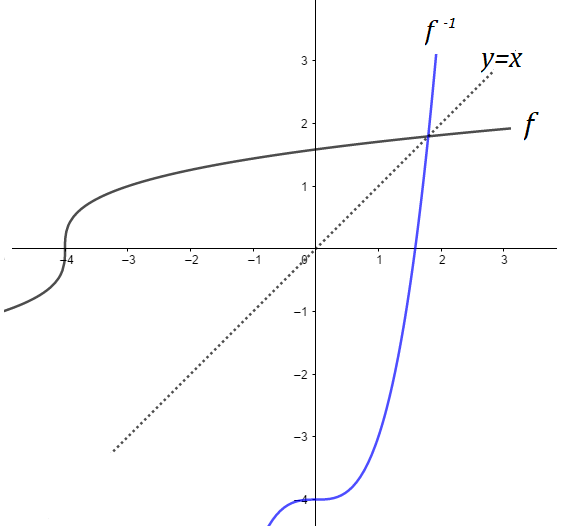
Esboçando o gráfico de ambas as funções, também percebemos uma simetria em relação à equação y=x:

Referências bibliográficas:

LIMA, Elon Lages. Um Curso de Análise: Volume 1. Rio de Janeiro: IMPA, 2017.

GUIDORIZZI, Hamilton L. Um Curso de Cálculo: Volume 1. Rio de Janeiro: Editora LTC, 2001.

Texto originalmente publicado em https://www.infoescola.com/matematica/funcao-inversa/