Multiplicação de um número real por uma matriz

Por Robison Sá

Nos trabalhos componentes da série de artigos sobre as matrizes já pudemos compreender e aplicar conceitos sobre os tipos de matrizes e suas propriedades básicas, matrizes opostas, igualdade de matrizes, adição e subtração de matrizes e agora, no presente trabalho, iremos abordar a multiplicação de um número real k por uma matriz A. Caso queira saber sobre a evolução histórica dos conceitos sobre as matrizes, consulte os outros artigos desta série e, em cada um deles, você irá perceber a importância de alguns grandes nomes da matemática na evolução desse campo indispensável a vários segmentos das atividades humanas.

Conceituando

Dada uma matriz A = (a_ij)_{m x n},e um número real k, temos que k.A é uma matriz B = (b_ij)_{m x n}, tal que b_ij = k.a_ij.
Em termos gerais, temos...

k.A = (k.a_ij)_{m x n} em que 1 ≤ i ≤ m e 1 ≤ j ≤ n

Exemplo 1

Representação genérica da multiplicação de k.A

A partir do conceito exibido anteriormente, podemos elaborar uma representação genérica do produto entre o número real k e uma matriz A quaisquer.

Vamos usar como exemplo a matriz A = (a_ij)_3x3 que será multiplicada por k, isto é, k.A.

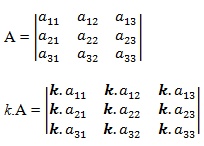
Propriedades da multiplicação de um número real k por uma matriz A

Sendo A, B, C e O (matriz nula) matrizes de mesmo tipo, valem as propriedades:

• 1 . A = A
• (- 1) . A = - A
• p . O = O
• 0 . A = O
• p . (A + B) = p . A + p . B
• (p + q) . B = p . B + q . B
• p . (q . A) = (p . q) . A

(YOUSSEF et al., 2005)

Aplicando os conceitos

Agora que sabemos os principais conceitos sobre a multiplicação de um número real por uma matriz, vamos responder mais uma questão para fixarmos a aprendizagem.

“Extraia dos momentos ruins a capacidade de revigorar-se, de renascer.”

(Robison Sá)

Referências bibliográficas:
SOUZA, Joamir Roberto de. Novo Olhar Matemática. – 1 ed. – São Paulo: FTD, 2010. – (Coleção novo olhar; v. 2)
YOUSSEF, Antonio Nicolau. Matemática: ensino médio, volume único / Antonio Nicolau Youssef, Elizabeth Soares, Vicente Paz Fernandez. – São Paulo: Scipione, 2005.

Texto originalmente publicado em https://www.infoescola.com/matematica/multiplicacao-de-um-numero-real-por-uma-matriz/