A fórmula do volume de esfera é dada pela seguinte constatação experimental: o volume de uma esfera de raio R é dois terços do volume de um cilindro de raio da base R e altura h = 2R (cilindro equilátero).
Volume de um cilindro equilátero (raio R e altura h = 2R):
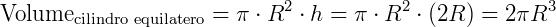
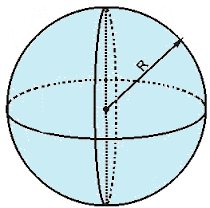 Volume da esfera de raio R:
Volume da esfera de raio R:
De acordo com a constatação experimental indicada acima, temos que:
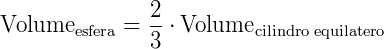
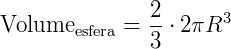

Exemplo:
Os planetas do sistema solar muitas vezes são representados como esferas. Na verdade, a maioria dos planetes são achatados nos polos, de modo que não são esferas perfeitas. Esse achatamento é praticamente nulo somente nos planetas Mercúrio e Vênus. Considerando que o raio equatorial de Mercúrio (rM) e o raio equatorial de Vênus (rV) são 2.439,7 km e 6.051,8 km, respectivamente. Calcule os volumes desses dois planetas:
Resposta:
Considerando que 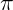 é aproximadamente 3,14:
é aproximadamente 3,14:
Volume de Mercúrio (VM): 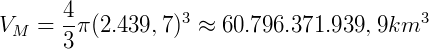
Volume de Vênus (VV): 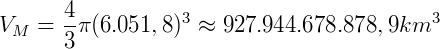
Texto originalmente publicado em https://www.infoescola.com/matematica/volume-da-esfera/