A ciência dos átomos ao início do século XX sofria uma série de transformações profundas em seus modelos explicativos. Rutherford propôs um modelo que considerava o átomo dotado de um núcleo denso e uma eletrosfera gigantesca, onde orbitavam elétrons.
Inicialmente, este novo modelo explicava satisfatoriamente a reflexão das partículas alfa, embora conflitasse com princípios intrínsecos à Física das partículas. Em determinado momento, cientistas questionaram como a eletrosfera manteria os elétrons em órbita e por que, após certo tempo estes elétrons não perderiam energia, caindo assim no núcleo do átomo.
Estudos do espectro eletromagnético, realizados por Robert Bünsen em meados do século XIX, indicaram uma possível elucidação destas questões. Bünsen e seu colaborador, Gustav Kirchhoff, estudaram os espectros de emissão de diversos gases e notaram que, além de não haver repetição no padrão das linhas espectrais, estas mesmas linhas eram separadas por espaços vazios.
Este fenômeno, inexplicável pelo modelo de Rutherford, uma vez que não se tinha plena convicção de como se comportava a eletrosfera, chamou a atenção de Niels Bohr (*1885 - † 1962). Segundo Bohr, a teoria proposta por Max Planck para o comportamento da luz (teoria dos quanta/quantização da energia) poderia dirimir as dúvidas que pairavam sobre o modelo atômico de Rutherford, além de explicar os espectros lineares de emissão atômica, observados por Bünsen.
Bohr afirmara que as órbitas presentes na eletrosfera seriam dotadas de um nível mínimo de energia, responsável pela manutenção dos elétrons em suas órbitas, impedindo assim que os mesmos perdessem energia e caíssem no núcleo. Estando estes elétrons em órbitas circulares (em relação ao núcleo), estes manteriam o nível mínimo de energia necessário a este movimento, denominando-se este nível mínimo de energia o estado fundamental do átomo.
Qualquer perturbação a este nível (fornecimento de energia térmica ou elétrica, por exemplo), causaria um aumento da energia potencial do elétron, fazendo com que o elétron saltasse de seu nível atual ao próximo nível de energia. E como este nível de energia maior seria “estranho” ao elétron, o mesmo retornaria ao seu nível original (de menor energia), liberando radiação no processo. A figura a seguir exemplifica o processo postulado por Bohr.
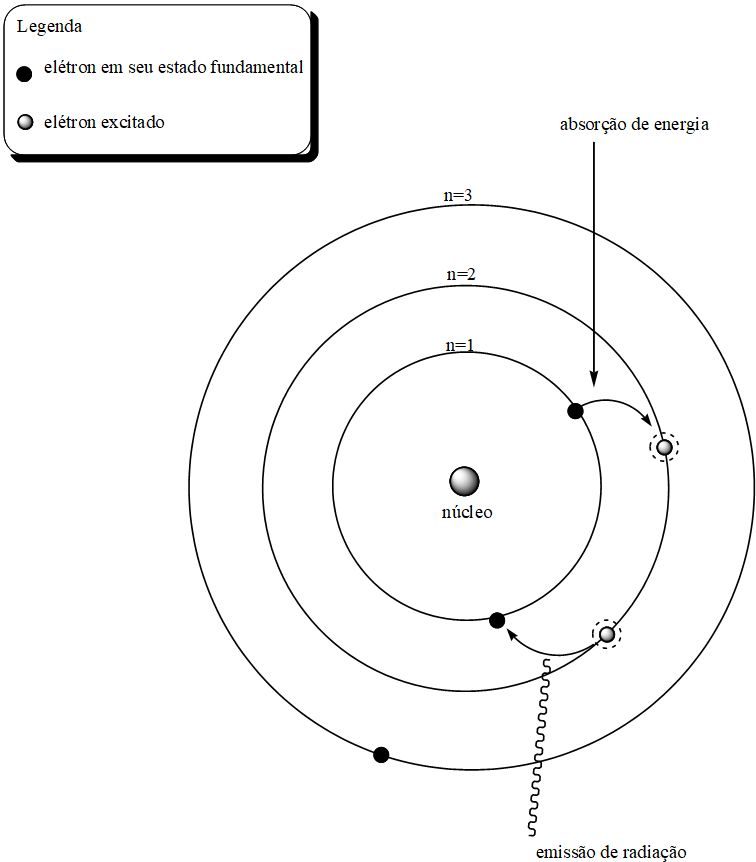
Modelo atômico de Bohr e a liberação de luz através dos espectros lineares.
A proposição de Bohr conseguia explicar o fenômeno dos espectros e respondia à questão do por que o átomo se mantém estável. A mecânica das órbitas também propunha que níveis mais distantes do núcleo apresentam maiores valores de energia, tendendo hipoteticamente ao infinito.
O modelo atômico de Bohr também previa a existência de órbitas cuja permanência do elétron não seria possível, denominando-as órbitas proibidas (presentes entre os níveis conhecidos de energia). Em tais órbitas os elétrons não poderiam permanecer e acabariam por emitir a energia excedente no traslado de um nível para o outro. Os níveis “permitidos” não emitiriam energia e, portanto, manter-se-iam estáveis.
A proposição do modelo de Niels Bohr considerava sete níveis ou camadas de energia (K, L, M, N, O, P, Q) sendo a camada K = n1; L = n2; M = n3...; onde teoricamente, os elétrons estariam orbitando em suas trajetórias esféricas.
O modelo de Bohr apresentava limitações quando se tratavam de elementos diferentes do hidrogênio, pois não conseguia explicar o espectro de raia, formado por elementos com mais elétrons, onde Sommerfeld propõe alterações ao modelo atômico de Bohr.
Leia também:
Referências:
LISBOA, J. C. F. Química, 1º ano: ensino médio. 1ª Ed. – São Paulo: Edições SM, 2010. (coleção Ser protagonista). p. 123 – 127.
FELTRE, R; YOSHINAGA, S. Atomística – 1ª Ed. – São Paulo: Moderna, 1970. p. 126 – 138.
FELTRE, R. Química Geral – 5ª Ed. – São Paulo: Moderna, 2000. p.98 – 106.
Texto originalmente publicado em https://www.infoescola.com/fisica/modelo-atomico-de-bohr/