A forma paramétrica de uma reta é mais uma de suas representações, assim como as formas: geral, segmentária e reduzida. O diferencial dessa representação é que podemos definir uma reta por meio de um parâmetro que chamamos de 𝑡, uma terceira variável, além das coordenadas cartesianas usuais. Sua definição é melhor compreendida quando o conceito de vetores já for apresentado. Vamos a sua definição:
Uma reta é chamada de parametrizada quando está na forma:
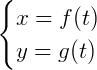
Onde 𝑓(𝑡) e 𝑔(𝑡) são funções do primeiro grau e dependentes do parâmetro 𝑡. Por exemplo, seja uma reta 𝑟 definida como:
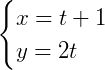
Se fizermos, para 𝑡 = 2, temos:
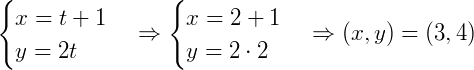
Vemos que o ponto (3,4) é um ponto desta reta.
É interessante transformarmos uma equação paramétrica em uma equação reduzida da reta e vice-versa. Vejamos como se faz:
1) Vamos obter a equação reduzida da reta parametrizada abaixo:
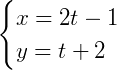
Primeiramente, podemos isolar 𝑡 de qualquer uma das duas equações. Vamos isolar da segunda:
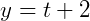
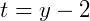
Isolado o parâmetro 𝑡 podemos substituir na primeira equação:
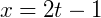
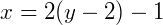
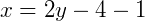
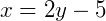
Por fim, encontramos a forma geral:
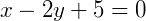
Agora, para a forma reduzida, que é aquela onde isolamos o 𝑦:
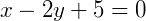
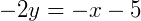
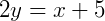
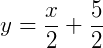
Obtendo assim a forma reduzida da reta.
2) Vamos por exemplo transformar a equação geral 𝑦 = 3𝑥 + 1 numa equação parametrizada. Primeiro, podemos escolher uma expressão em função de 𝑡 arbitrária para substituir em qualquer uma das variáveis, desde que essa função seja do primeiro grau. Sendo assim, por praticidade vamos escolher 𝑦 = 3𝑡 + 4:
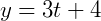
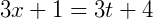
Agora, isolamos 𝑥 para descobrirmos o parâmetro em função de 𝑡 para 𝑥:
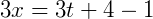
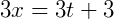
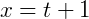
Agora, temos a nossa reta parametrizada em funções de 𝑡 para 𝑥 e 𝑦:
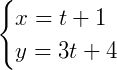
Podemos ainda fazer o processo inverso para testarmos se a parametrização está de acordo com a equação reduzida da reta, isolando 𝑡 em 𝑥 neste caso:
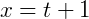
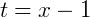
Substituindo em 𝑦:
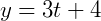
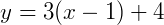
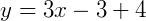
Por fim, reencontrando a equação reduzida da expressão:
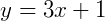
Num estudo mais aprofundado de parametrizações, é possível que qualquer reta ou curva no espaço possa ser parametrizada em funções de 𝑡, parábolas, hipérboles, elipses entre outras curvas. Vale a pena pesquisar sobre esse tema,onde a área da matemática que, inicialmente, explora as parametrizações de curvas, é chamada de Geometria Diferencial.
Referências Bibliográficas:
WINTERLE, Paulo. Vetores e Geometria Analítica. São Paulo: Pearson Makron Books,2000.
DANTE, Luiz Roberto. Matemática: Contextos & Aplicações - Volume 3. São Paulo: Editora Ática, 2011.
Texto originalmente publicado em https://www.infoescola.com/matematica/equacao-parametrica-da-reta/