Equação reduzida da reta

Quando estudamos função, verificamos que uma função do 1º grau é definida por uma expressão algébrica do 1º grau com duas variáveis que o seu gráfico é uma reta.

Reciprocamente, podemos dizer que uma linha reta é representada por uma equação do 1º grau com duas variáveis. Nesta unidade, estudaremos a equação reduzida da reta.

Equação Reduzida da Reta

Já sabemos que a equação da reta, se forem conhecidos um ponto P(x₁, y₁) da reta e o coeficiente angular m, é dada por:

$y-y_1=m(x-x_1)$

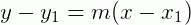
Se escolhermos o ponto particular de coordenadas (0, n) para o ponto (x₁, y₁), teremos a equação:

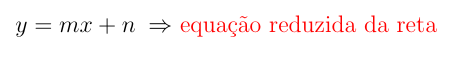
O número real n, que é a ordenada do ponto onde a reta corta o eixo y, é chamado coeficiente linear da reta.

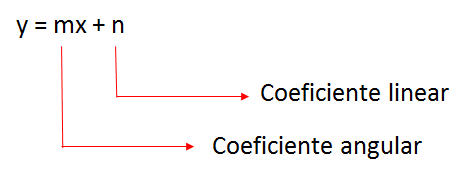
Então:

Exercícios resolvidos

1º) Determine a forma reduzida da equação da reta que passa pelo ponto P = (-3, 7) e tem coeficiente angular igual a 2.

Resolução: m = 2, x₁ = -3, y₁ = 7 e Q = (x, y)

Substituindo na equação fundamental da reta, temos:

y – 7 = 2 . [ x - (-3)] ⇒

y - 7 = 2x + 6 ⇒

y = 2x + 13

2º) Obter a forma reduzida da equação da reta que passa pelos pontos A = (2, 1) e B = (4, 6) e destacar o coeficiente angular e o coeficiente linear desta reta.

Resolução: Cálculo do coeficiente angular:

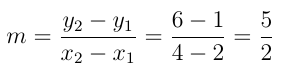
Vamos obter a equação reduzida da reta, temos:

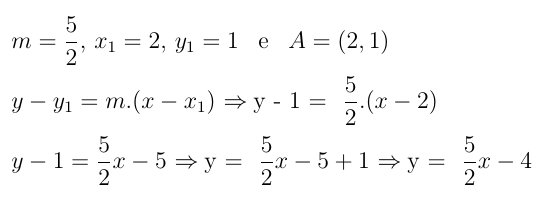
Coeficiente angular da reta:

$m=\frac{5}{2}$

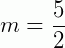
Coeficiente linear da reta:

$n=-4$

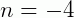
3º) Uma reta tem como equação: 2x + 3y – 6 = 0. Determine o coeficiente angular e o coeficiente linear dessa reta.

Resolução: Escrevemos a equação reduzida dessa reta, para que os coeficientes angular e linear fiquem evidentes:

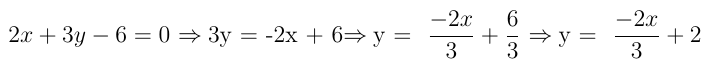
Assim, o coeficiente angular é 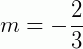$m=-\frac{2}{3}$ e o coeficiente linear é n = 2.

4º) Escrever a equação reduzida da reta representada no gráfico abaixo. Em seguida, destacar os coeficientes angular e linear dessa reta.

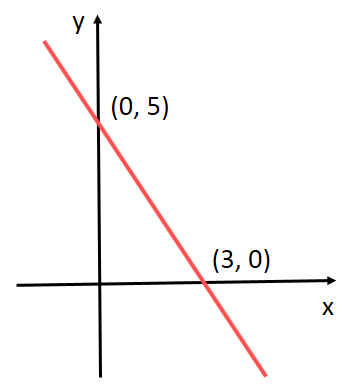
Resolução: Sejam A = (0, 5) e B = (3, 0).

Vamos calcular o coeficiente angular:

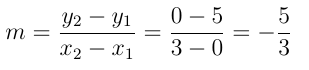
Considerando o ponto B = (3, 0), temos:

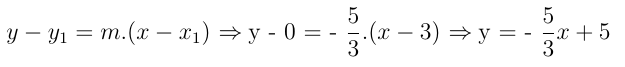
Leia também:

• Equações da reta
• Equação fundamental da reta
• Equação paramétrica da reta
• Equação segmentária da reta
• Equação geral da reta

Referências bibliográficas:

1. MURAKAMI, C.; IEZZI, G. Fundamentos de Matemática Elementar: Conjuntos. Funções. Vol. 1. 8ª Ed. Editora: Atual. 2004.

2. LIMA, E. L., et al. A Matemática do Ensino Médio. 9ª ed. Rio de Janeiro: SBM, 2006. v.1

3. DANTE, Luis Roberto. Matemática: contexto e aplicações. Volume único. São Paulo: Editora Ática, 2009.

Texto originalmente publicado em https://www.infoescola.com/matematica/equacao-reduzida-da-reta/