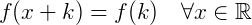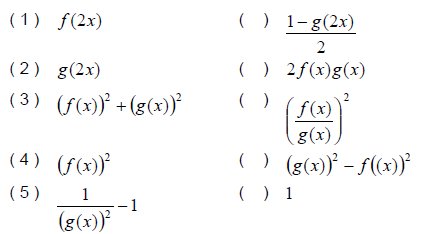As funções trigonométricas são funções periódicas, ou seja, na sua representação gráfica as funções se caracterizam pela repetição de um padrão. Este padrão chamamos de período. Veja abaixo a definição formal de função periódica:
Uma função f: A→B é dita periódica se existir um número k > 0 onde o menor valor de k que satisfaz a condição abaixo é chamado de período:
Tendo em vista que os valores das funções trigonométricas têm como parâmetro a sua representação no ciclo trigonométrico, então os períodos de cada função estarão limitados à cada ciclo completo no eixo trigonométrico.
Conteúdo deste artigo
Função seno
A função seno é definida como uma função 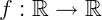 tal que:
tal que:
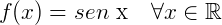
Representação no ciclo trigonométrico:
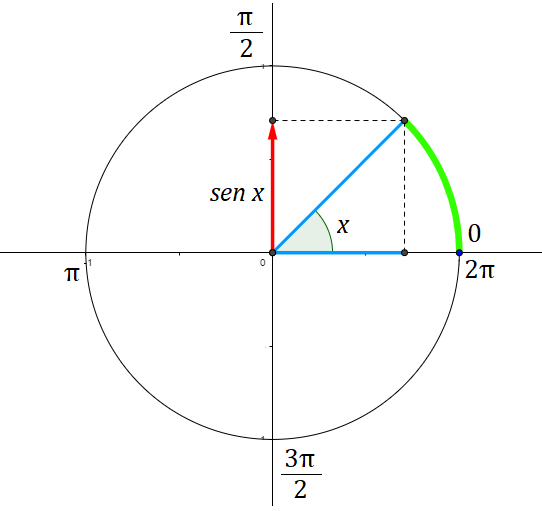
Imagem: A imagem da função seno é o intervalo [-1, 1]. Isso é um fato conhecido pois os valores que o seno pode assumir para qualquer valor de x podem variar apenas de -1 e 1.
Período: O período da função seno é 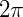 pois se
pois se 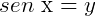 (qualquer valor de x teremos um valor em y) então
(qualquer valor de x teremos um valor em y) então 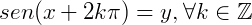 , terá a mesma imagem no ciclo, ou seja:
, terá a mesma imagem no ciclo, ou seja:
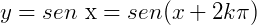
Exemplo 1) k=1 e 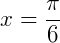 , temos que:
, temos que:
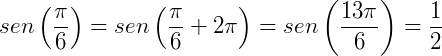
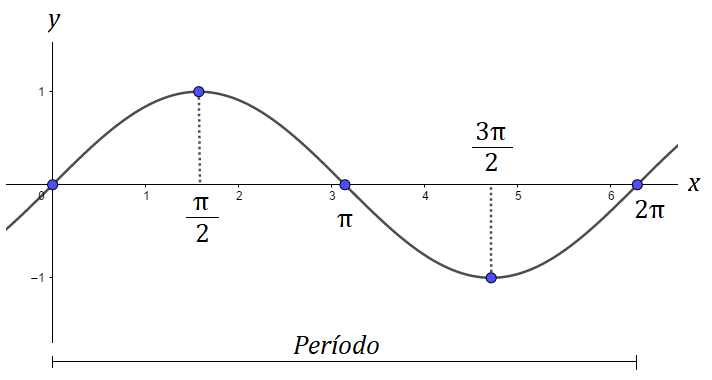
Gráfico:
Função cosseno
A função cosseno é definida como uma função 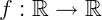 tal que:
tal que:
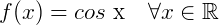
Representação no ciclo trigonométrico:
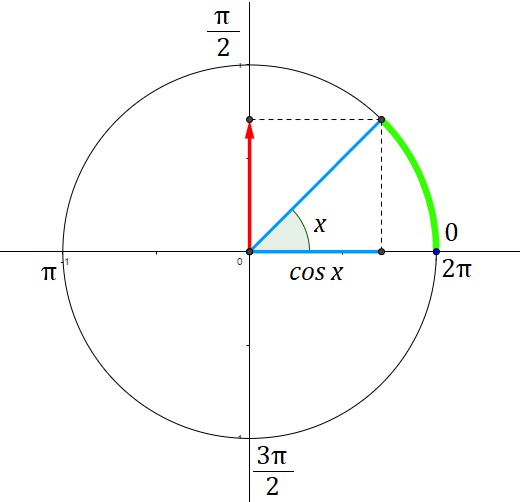
Imagem: A imagem da função cosseno é o intervalo [-1, 1]. Isso é um fato conhecido pois os valores que o cosseno pode assumir para qualquer valor de x podem variar apenas de -1 e 1.
Período: O período da função cosseno é 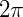 pois se
pois se 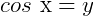 (qualquer valor de x teremos um valor em y) então
(qualquer valor de x teremos um valor em y) então 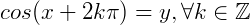 , terá a mesma imagem no ciclo, ou seja:
, terá a mesma imagem no ciclo, ou seja:
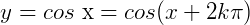
Exemplo 2) k=2 e 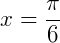 , temos que:
, temos que:
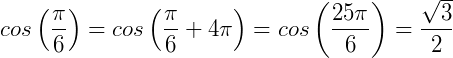
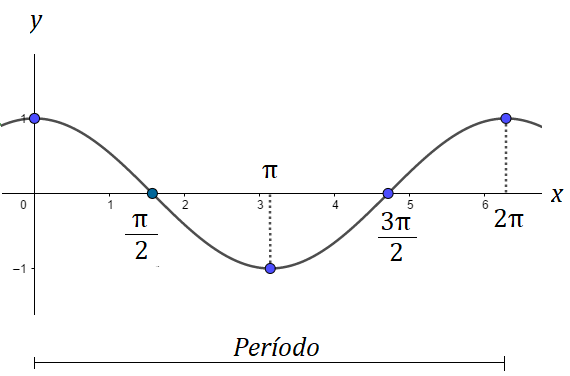
Gráfico:
Função tangente
A função tangente é definida como uma função 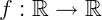 tal que:
tal que:
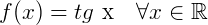
Representação no ciclo trigonométrico:
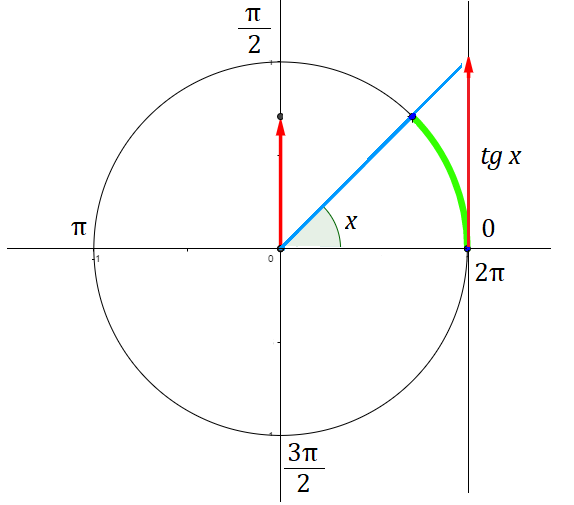
Domínio: O domínio da função tangente é diferente das funções seno e cosseno. Logo, o domínio da função será dado por 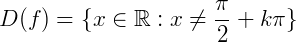 onde percebemos que não existem valores para a tangente quando a sua representação no ciclo estiver no eixo dos senos. Classificamos a função tangente como periódica e também assintótica.
onde percebemos que não existem valores para a tangente quando a sua representação no ciclo estiver no eixo dos senos. Classificamos a função tangente como periódica e também assintótica.
Imagem: A imagem da função tangente é o próprio conjunto dos reais 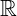 , ou seja, para qualquer valor de x existe y real.
, ou seja, para qualquer valor de x existe y real.
Período: O período da função tangente é 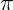 . Então dizemos:
. Então dizemos: 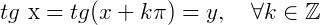 , terá a mesma imagem no ciclo, ou seja:
, terá a mesma imagem no ciclo, ou seja:
Exemplo 2) k=3 e 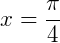 , temos que:
, temos que:
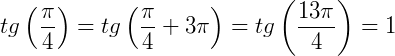
Gráfico:
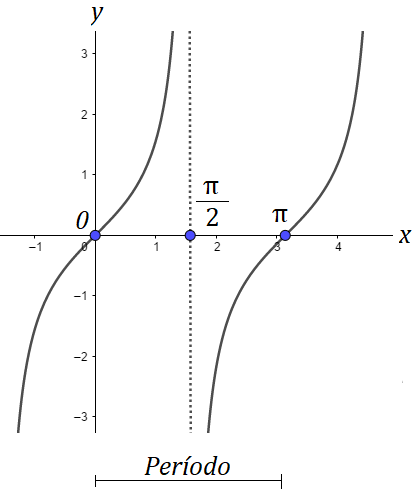
Note que no ponto 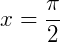 o gráfico não tem nenhuma representação em y, o que torna a função tangente uma assíntota nos pontos onde
o gráfico não tem nenhuma representação em y, o que torna a função tangente uma assíntota nos pontos onde 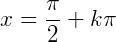 .
.
Referências Bibliográficas:
IEZZI, Gelson. Fundamentos de Matemática Elementar – Volume 3 - Trigonometria: São Paulo: Editora Atual, 2013.
GUIDORIZZI, Hamilton L. Um Curso de Cálculo: Volume 1. Rio de Janeiro: Editora LTC, 2001.
Texto originalmente publicado em https://www.infoescola.com/matematica/funcoes-trigonometricas/