Os números complexos formam um conjunto numérico que é mais abrangente que os números reais. Eles surgiram após inúmeros estudos, sobretudo após tentativas de se resolver equações do segundo e do terceiro grau. Nessa época, os matemáticos se depararam raízes quadradas de números negativos, que não podem ser expressas no conjunto dos números reais. Assim, os matemáticos passaram a denotar essas raízes usando a letra “i”. A base principal foi adotar 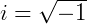 .
.
Conteúdo deste artigo
- Definição
- Adição de números complexos
- Subtração de números complexos
- Multiplicação de números complexos
- Divisão de números complexos
- Argumento e módulo de um número complexo
- Argumento de Z
- Módulo de Z
- Forma trigonométrica de um número complexo
- Produto de números complexos na forma polar
- Potência de um número complexo
- Exercícios e questões de vestibulares
Definição
Quando vamos solucionar equações do tipo 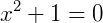 , nos deparamos com
, nos deparamos com 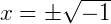 . Como não existe raiz quadrada de número negativo no conjunto dos números reais, convencionou-se utilizar a notação
. Como não existe raiz quadrada de número negativo no conjunto dos números reais, convencionou-se utilizar a notação 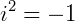 para representar esse número negativo. Com isso, o resultado da equação anterior seria
para representar esse número negativo. Com isso, o resultado da equação anterior seria 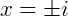 . Esse número “i” é conhecido como unidade imaginária.
. Esse número “i” é conhecido como unidade imaginária.
Assim, um número complexo, que chamamos de Z, tem a forma
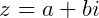 ,
, 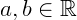
Chamamos o número a de parte real, Re(Z) = a, e b de parte imaginária, Im(Z) = b. Esta notação é chamada de forma algébrica.
Adição de números complexos
A adição de números complexos é realizada através da adição dos termos semelhantes, ou seja, somamos as partes reais de cada número e depois as partes imaginárias. Sejam 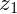 e
e 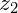 dois números complexos, tais que:
dois números complexos, tais que: 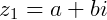 e
e 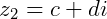 .
.
Definiremos a adição de 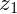 e
e 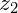 da seguinte forma:
da seguinte forma:
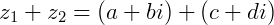
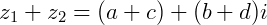
Exemplo:
Se 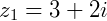 e
e 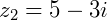 a soma será:
a soma será:
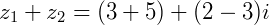
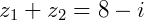
Subtração de números complexos
A subtração de números complexos é análoga à adição. Calculamos a diferença entre as partes reais de cada número e depois as partes imaginárias.
Sejam 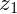 e
e 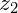 dois números complexos, tais que:
dois números complexos, tais que: 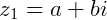 e
e 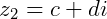 .
.
Definiremos a subtração de 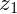 e
e 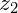 da seguinte forma:
da seguinte forma:
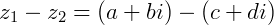
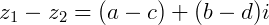
Exemplo:
Se 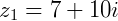 e
e 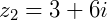 a diferença será:
a diferença será:
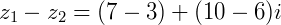
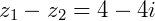
Multiplicação de números complexos
Para multiplicar números complexos utilizamos o mesmo método adotado na expansão de um produto notável, multiplicando cada termo do primeiro fator por todos os membros do segundo fator. Assim:
Sejam 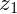 e
e 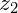 dois números complexos, tais que:
dois números complexos, tais que: 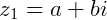 e
e 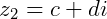 .
.
Definiremos a multiplicação de 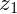 e
e 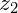 da seguinte forma:
da seguinte forma:
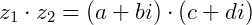
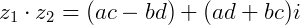
Exemplo:
Se 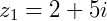 e
e 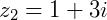 o produto será:
o produto será:
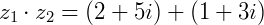
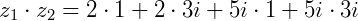
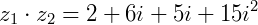
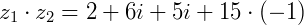
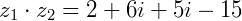
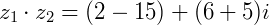
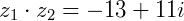
Divisão de números complexos
Para dividir números complexos multiplicamos o dividendo e o divisor pelo conjugado do divisor. O conjugado de um número complexo 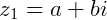 será
será 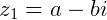 .
.
Sempre que multiplicamos um número complexo pelo seu conjugado, o denominador será um número real.
Sejam 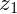 e
e 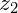 dois números complexos, tais que:
dois números complexos, tais que: 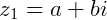 e
e 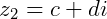
Definiremos a divisão de 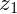 e
e 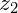 da seguinte forma:
da seguinte forma:
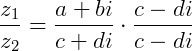
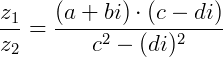
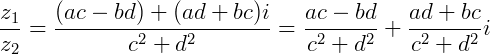
Exemplo
Se 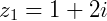 e
e 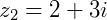 a divisão será:
a divisão será:
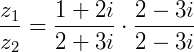
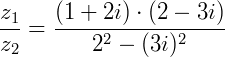
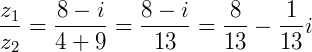
Argumento e módulo de um número complexo
Podemos representar um número complexo em um sistema de coordenadas. Esse sistema de coordenadas é chamado de Plano de Argand-Gauss. É composto por dois segmentos de reta perpendiculares. O segmento horizontal comporta as partes reais dos números complexos e o segmento vertical, as partes imaginárias. Como exemplo, observe como será representado o número complexo 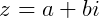 no Plano de Argand-Gauss:
no Plano de Argand-Gauss:
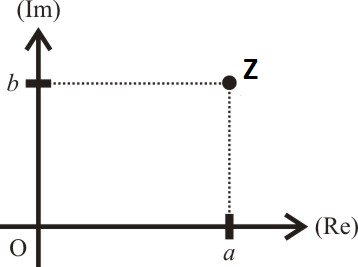
O segmento de reta OZ é chamado de módulo do número complexo, representado por |z|. Na figura abaixo, o ângulo entre o eixo Ox e o segmento OZ é chamado de argumento de Z, representado por 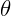 .
.
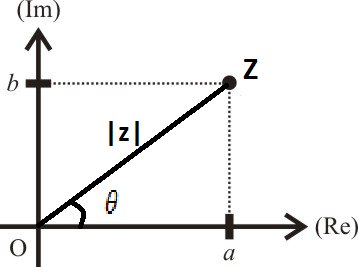
Argumento de Z
No Triângulo retângulo formado pelos vértices OâZ, temos que:
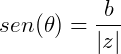
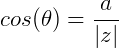
Sendo 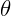 o argumento de Z.
o argumento de Z.
Para encontrar o argumento de Z, podemos utilizar 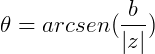 ou
ou 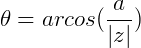 .
.
Módulo de Z
Aplicando o teorema de Pitágoras teremos:
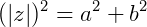
Então:
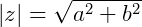
Forma trigonométrica de um número complexo
Cada número complexo pode ser expresso em função do seu módulo e argumento. Quando isso acontece dizemos que o número complexo está na forma trigonométrica ou polar.
Considere o número complexo 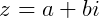 , em que z ≠ 0,
, em que z ≠ 0,
Como vimos anteriormente:
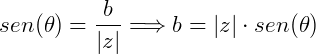
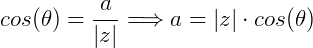
Substituindo os valores de a e b no complexo 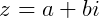 .
.
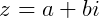
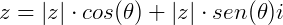
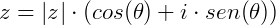
Produto de números complexos na forma polar
Considere dois números complexos na forma polar:
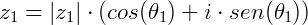
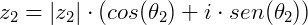
O produto entre será:
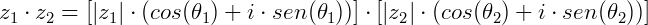
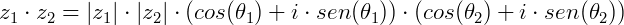
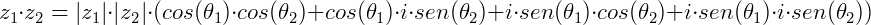
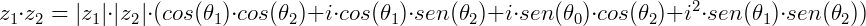
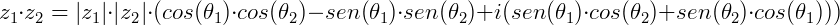
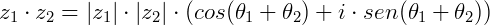
Assim, para multiplicar dois números complexos na forma polar, basta multiplicar seus módulos e somar seus argumentos.
Exemplo:
Se 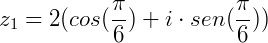 e
e 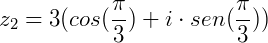 :
:
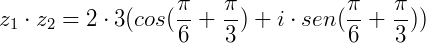
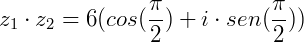
Potência de um número complexo
Como vimos anteriormente, para multiplicar números complexos, basta multiplicar seus módulos e somar seus argumentos.
Se multiplicarmos um número complexo Z por ele mesmo n vezes, teremos:
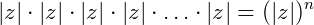
e
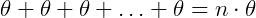
Assim, elevando Z a uma potência n, teremos que:
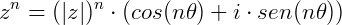
Exemplo:
Calcular 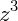 , sendo
, sendo 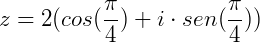 .
.
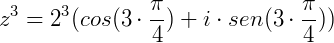
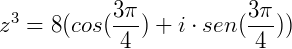
Texto originalmente publicado em https://www.infoescola.com/matematica/numeros-complexos/