Para uma melhor compreensão da definição de número irracional, é necessário que sejam apresentadas algumas propriedades dos números racionais. Definimos um número racional como qualquer número que possa ser escrito da forma 
, com p sendo um número inteiro e q um número inteiro diferente de zero. Formalmente escrevemos o conjunto dos números racionais 
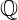da seguinte maneira:
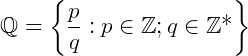
Então, podemos dizer que qualquer fração (ou razão) que possa ser obtida pela divisão de dois números inteiros nessas condições é chamado de número racional. A questão agora é: Como sabemos se um número é racional?
Abaixo temos alguns casos possíveis para a sua representação:
1) Frações (redutíveis ou não): 
, 
, 
, ...
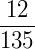2) Números decimais finitos: 4,5 ; 7,32 ; 2,31 ; ....
3) Números mistos: 
, 
, ...
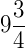4) Dízimas periódicas: 0,7777... ou 0,7 ; 0,393939... ou 0,39; 13,147147147... ou 13,147
Há ainda alguns números que possuem representação decimal, porém não sabemos, de pronto, se ele pode ou não ser um racional. Vamos analisar por exemplo o número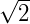 
, que possui o seguinte valor aproximado.
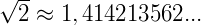
Ora, não podemos afirmar que o número possui uma dízima periódica, pois não sabemos se a representação decimal irá repetir um padrão (isso pode ocorrer na 20ª casa decimal ou na 100.000ª). Para definirmos números que estão nesta forma, digamos, incerta, devemos recorrer ao Teorema Fundamental da Aritmética para classificá-lo.
Teorema Fundamental da Aritmética (T.F.A.): Todo número inteiro maior do que 1, 0 e -1 pode ser escrito (ou decomposto) pelo produto de fatores primos de forma única.
Exemplos:
- O número 15 pode ser escrito como (3.5), onde 3 e 5 são primos;
- 28 = 2.2.7 (2 e 7 são primos)
- 135 = 3.3.3.5
Se elevarmos qualquer número inteiro a uma potência de qualquer valor (2, 3, 4, ...) o T.F.A. continuará valendo, por exemplo:
- 152 = 32.52 = 9.25 = 225
- 282 = 22.22.72 = 4.4.49 = 784
- 1353 = 33. 33. 33.53 = 27.27.27.125 = 2460375
Podemos então generalizar. Qualquer número inteiro x pode ser escrito da seguinte forma:
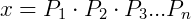
E se elevarmos esse número inteiro a qualquer potência de valor m teremos:
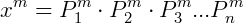
Sendo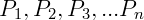 
números primos.
Voltando ao 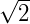, temos uma dúvida a respeito de sua classificação. Porém, podemos partir da premissa de que ele é um número racional. Se ele for racional, então pode ser escrito da forma . E se ele pode ser obtido pela razão entre dois inteiros então é válido dizer que:
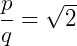
Então uma nova pergunta surge: Existe um número racional que elevado ao quadrado seja igual a dois? Para responder essa pergunta, devemos então operar ambos os lados da equação, o que nos resulta em:
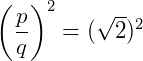
Como o índice da raiz a direita também é dois (raiz quadrada), então anulamos a raiz, por definição:
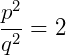
O que nos garante escrever que:
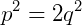
Como p é um número inteiro, então ele obedece ao T.F.A. quando elevado a uma potência e também pode ser decomposto em fatores primos. Mas note que na expressão, a potência de 2, que é igual a um, não acompanha a definição do T.F.A. o que é um absurdo! Elevando qualquer inteiro a uma potencia m, os primos que o compõe também devem ser elevados a mesma potencia m, o que não ocorre com 2 nesta expressão e sim apenas com o inteiro q. Concluindo então que não pode ser escrito da forma p/q, logo ele não é um número racional, e sim, Irracional. Em outras palavras, não existem dois inteiros p e q que quando divididos têm como resultado 1,414213562...
Formalmente definimos então um Número Irracional, que é representado por I, como sendo um número que não pode ser obtido da forma p/q, com p e q inteiros. Alguns exemplos de números irracionais são:
1. Raízes quadradas de números primos: ,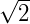 
, 
...
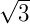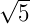2. Algumas constantes: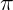 
, e, ln 2, ln 3
Referências Bibliográficas:
MILIES, César P.; COELHO, Sônia P. Números, Uma Introdução à Matemática. São Paulo: EDUSP, 2013.
LIMA, Elon Lages. Um Curso de Análise: Volume 1. Rio de Janeiro: IMPA, 2017.
Texto originalmente publicado em https://www.infoescola.com/matematica/numeros-irracionais/