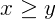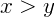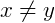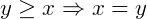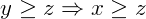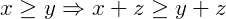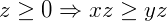Antes de apresentarmos o conteúdo de sistemas de inequações é imprescindível que o leitor conheça os conceitos de intervalos reais, inequações do 1º grau e sistemas de equações.
Um sistema de inequações obedece às mesmas propriedades de um sistema de equações, sendo que o mesmo é formado por duas ou mais equações de uma variável e as expressões são desigualdades. A solução de um sistema de inequações também será dada por um intervalo real, ou seja, um conjunto solução. Vamos relembrar alguns conceitos de inequações do primeiro grau:
- Se
 , dizemos que x é maior ou igual a y;
, dizemos que x é maior ou igual a y; - Se
 , então x é maior do que y;
, então x é maior do que y; - Se
 , dizemos que x é diferente de y.
, dizemos que x é diferente de y.
Agora, algumas propriedades a respeito das desigualdades:
- Reflexiva:

- Antissimétrica:
 e
e 
- Transitiva:
 e
e 
- Compatibilidade com a Adição:

- Compatibilidade com a Multiplicação:
 e
e 
Resolvendo um sistema de inequações
Exemplo 1) Vamos encontrar o conjunto solução do sistema dado por:
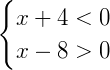
Obtendo o valor de x nas expressões separadamente temos:
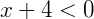
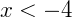
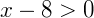
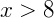
O nosso conjunto solução é dado pela intersecção dos dois intervalos acima. Como podemos observar, não há elementos presentes simultaneamente em ambos os intervalos, então a solução é um conjunto vazio.

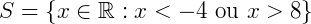
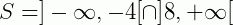
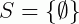
Exemplo 2) Agora vamos solucionar o sistema abaixo:
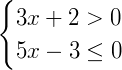
Solucionando separadamente temos:
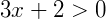
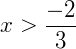

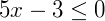
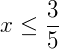

Neste caso perceba que o conjunto solução desta equação será o intervalo:

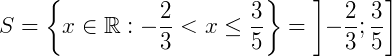
Exemplo 3) Um sistema de inequações também pode ser escrito de uma forma linear, contendo duas desigualdades. Veja abaixo:
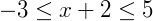
Neste caso podemos reescrever como:
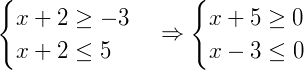
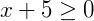
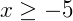

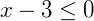
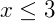

Sendo assim, o nosso conjunto solução será dado por:

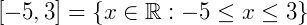
Referências Bibliográficas:
LIMA, Elon Lages. Um Curso de Análise: Volume 1. Rio de Janeiro: IMPA, 2017.
GUIDORIZZI, Hamilton L. Um Curso de Cálculo: Volume 1. Rio de Janeiro: Editora LTC, 2001.
Texto originalmente publicado em https://www.infoescola.com/matematica/sistemas-de-inequacoes/