Equações da Reta

Em matemática, a geometria analítica estuda equações e suas representações por meio de um sistema de coordenadas cartesianas. Concentrando-se no estudo das retas e a sua representação no plano cartesiano, a equação da reta nos permite diferentes formas de representação. Algumas propriedades e condições são elementares para interpretar o seu comportamento. Vejamos exemplos:

Equação Reduzida da Reta

Uma equação linear pode ser representada no plano por uma linha, ou uma reta, no plano cartesiano em duas dimensões, onde na forma reduzida é descrita por:

$y=mx+b$

Onde: m é o coeficiente angular da reta, b é o ponto de intersecção com o eixo y, também chamado de coeficiente linear e x é a variável aleatória. No plano cartesiano temos:

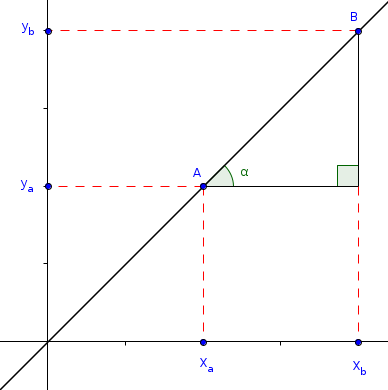
Onde A e B são dois pontos tais que A=(x_a, y_a) e B=(x_b, y_b). O valor do coeficiente angular da reta m é dado pela relação:

$m=tan(\alpha)=\frac{y_b-y_a}{x_b-x_a}$

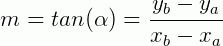
O que nos possibilita escrever outra forma da equação geral da reta, dados 2 pontos, que é dada por:

$y_b-y_a=m(x_b-x_a)$

A equação reduzida da reta também é chamada de equação fundamental da reta.

Equação Geral da Reta

Equação geral da reta é obtida quando isolamos a equação reduzida da reta para a seguinte forma:

$ax+by+c=0$

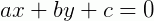
Onde: 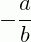$-\frac{a}{b}$ é o coeficiente angular da reta, 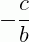$-\frac{c}{b}$ é o ponto coeficiente linear e x é a variável aleatória.

Equação Matricial da Reta

Outra maneira de representarmos a equação de uma reta é pela forma de um determinante de uma matriz. Dados dois pontos A=(x_a, y_a) e B=(x_b, y_b), temos:

$\begin{bmatrix}x&y&1\\x_a&y_a&1\\x_b&y_b&1\end{bmatrix}=0$

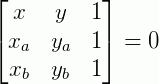
Resolvendo este determinante pelo método de Sarrus, temos:

$\begin{bmatrix}x&y&1\\x_a&y_a&1\\x_b&y_b&1\end{bmatrix}=$

$=x\cdot y_a+y\cdot x_b + x_a\cdot y_b -y_a\cdot x_b-x\cdot y_b-y\cdot x_a=0$

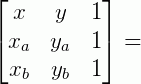
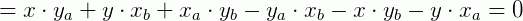
De um modo geral, esta igualdade acima pode ser relacionada de forma equivale a:

$y-y_a=m(x-x_a)=\frac{\Delta y}{\Delta x}(x-x_a)=\frac{(y_b-y_a)}{(x_b-x_a)}(x-x_a)$

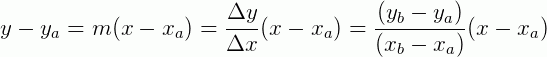
Onde Δx e Δy são as variações (y_b-y_a) e (x_b-x_a) respectivamente.

Equação Paramétrica da Reta

A forma paramétrica de uma reta é mais uma de suas representações, assim como as formas: geral, segmentária e reduzida. O diferencial dessa representação é que podemos definir uma reta por meio de um parâmetro que chamamos de , uma terceira variável, além das coordenadas cartesianas usuais. Sua definição é mais bem compreendida quando o conceito de vetores já for apresentado. Vamos a sua definição:

Uma reta é chamada de parametrizada quando está na forma:

$\begin{cases}x=f(t)\\y=g(t)\end{cases}$

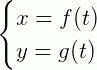
Onde f(t) e g(t) são funções do primeiro grau que são dependentes do parâmetro t.

Leia também:

• Posições relativas de duas retas

Referências bibliográficas:

WINTERLE, Paulo. Vetores e Geometria Analítica. São Paulo: Pearson Makron Books, 2000.

Texto originalmente publicado em https://www.infoescola.com/geometria-analitica/equacoes-da-reta/