De modo prático, o volume de um sólido geométrico é a medida da região do espaço limitada por sua superfície. Em termos da Matemática, volume de um sólido é um número real positivo associado ao sólidos de forma que:
- sólidos congruentes têm volumes iguais.
- se um sólido S é a reunião de dois sólidos S1 e S2 que não têm pontos internos comuns, então o volume de S é a soma dos volumes de S1 e S2.
Observação: Os sólidos são medidos por uma unidade que, em geral, é um cubo. Portanto, o volume desse cubo é 1. Se sua aresta mede 1 cm, seu volume será 1 cm³. Se sua aresta medir 1 m, seu volume será 1 m³.
Veja abaixo expressões de volume de alguns sólidos.
Conteúdo deste artigo
Cubo
Expressão do volume do cubo: 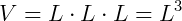
Leia mais: volume do cubo
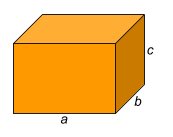
Paralelepípedo
Expressão do volume do paralelepípedo: 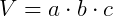
Leia mais: volume do paralelepípedo
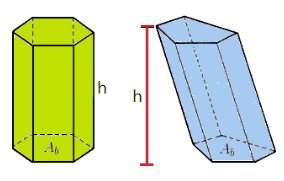
Prisma
Expressão do volume do prisma: 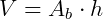
Leia também: volume do prisma
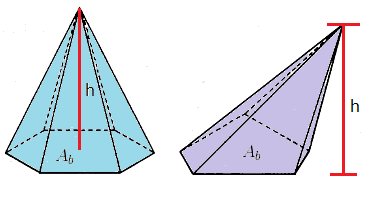
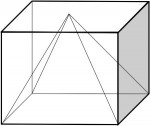
Pirâmide
Expressão do volume da pirâmide: 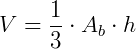
Leia também: volume da pirâmide
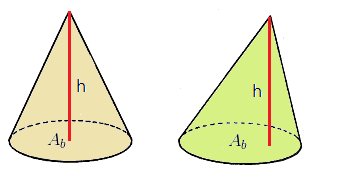
Cone
Expressão do volume do cone: 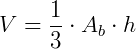
Leia também: volume do cone
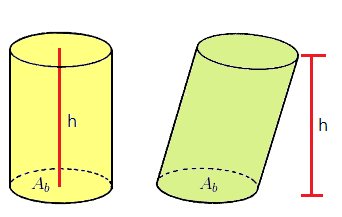
Cilindro
Expressão do volume do cilindro: 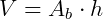
Leia também: volume do cilindro
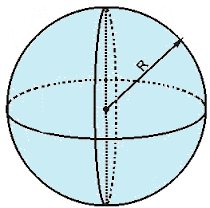
Esfera
Expressão do volume da esfera: 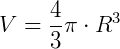
Leia também: volume da esfera
Texto originalmente publicado em https://www.infoescola.com/matematica/volume-de-solidos-geometricos/
 Os papiros mostram que os egípcios antigos possuíam diversos conhecimentos matemáticos. Eles sabiam que o volume da pirâmide equivale a um terço do volume do prisma que a contém. A maior pirâmide egípcia, Quéops, construída por volta de 2560 a.C., tem uma altura aproximada de 140 metros e sua base é um quadrado com lados medindo aproximadamente 230 metros. Logo, o volume da pirâmide de Quéops é de aproximadamente (em milhões de metros cúbicos):
Os papiros mostram que os egípcios antigos possuíam diversos conhecimentos matemáticos. Eles sabiam que o volume da pirâmide equivale a um terço do volume do prisma que a contém. A maior pirâmide egípcia, Quéops, construída por volta de 2560 a.C., tem uma altura aproximada de 140 metros e sua base é um quadrado com lados medindo aproximadamente 230 metros. Logo, o volume da pirâmide de Quéops é de aproximadamente (em milhões de metros cúbicos):