Divisão de polinômios - Matemática

Dados dois polinômios A(x) e B(x) ≠ 0, a divisão do polinômio A(x) por B(x) é encontrar dois polinômios Q(x) e R(x) de forma que se verifiquem as seguintes condições:

A(x) = B(x) . Q(x) + R(x)

grau de R(x) < grau de B(x)

A(x) é o dividendo, B(x) é o divisor, Q(x) é o quociente e R(x) é o resto da divisão.

Se R(x) = 0 (polinômio nulo), temos que:

A(x) = B(x) . Q(x)

$\frac{A(x)}{B(x)}=Q(x)$

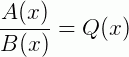
Dizemos, nesse caso, que A(x) é divisível por B(x).

O método geral utilizado para se efetuar a divisão de dois polinômios é apresentado a seguir.

Como exemplo, vamos dividir o polinômio A(x) = 2x⁴ – 3x³ + x – 1 por B(x) = x² – 2x + 3.

Seguiremos o seguinte roteiro:

1º) Escrevemos os dois polinômios em ordem decrescente de grau.

2º) Completamos o dividendo, caso falte algum termo de grau intermediário, através do coeficiente zero.

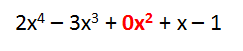
3º) Utilizando o mesmo algoritmo da divisão numérica, dividimos o 1º termo de A(x) pelo 1º termo de B(x).

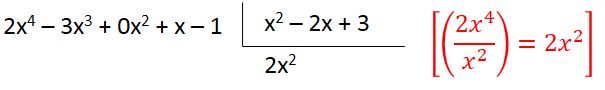
4º) Multiplicamos o quociente obtido por B(x) e subtraímos o resultado de A(x), encontrando o 1º resto parcial.

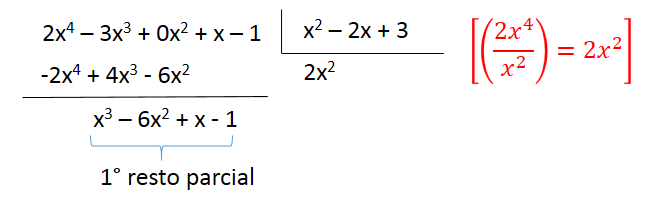
5º) Dividimos o 1º termo do 1º resto parcial pelo 1º termo de B(x). Multiplicamos o quociente obtido por B(x) e subtraímos do 1º resto parcial, obtendo o 2º resto parcial.

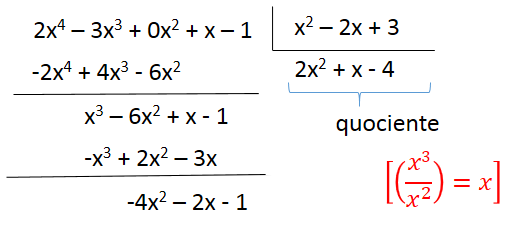
6º) Repetimos esse procedimento até que o grau do resto seja menor que o grau do divisor.

Observe que o resto (-10x + 11) possui grau menor que o grau do divisor (x² – 2x + 3).

Temos, portanto:

Quociente: Q(x) = 2x² + x - 4

Resto: R(x) = -10 x + 11