Polinômios

Chamamos de polinômio ou expressão polinomial, onde 𝑥 é uma variável complexa, qualquer expressão que tenha a forma:

$a_nx^n+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+...+a_1x^1+a_0x^0$

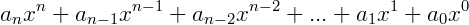
Ou ainda, pela notação de somatório:

$\displaystyle\sum_{i=0}^na_ix^i$

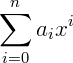
Onde 𝑎_𝑛, 𝑎_𝑛−1, 𝑎_𝑛−2, ..., 𝑎₁ e 𝑎₀ são as constantes que chamamos de coeficientes do polinômio e 𝑥^𝑛, 𝑥^𝑛−1, ..., 𝑥⁰ são as variáveis complexas da expressão.

Grau de um polinômio

O grau de um polinômio é classificado pelo valor do expoente 𝑛 na variável 𝑥 do polinômio, sendo que 𝑛 deve ser um inteiro positivo e maior ou igual a zero, ou seja: 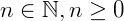$n\in\mathbb{N}, n\geq 0$.

Exemplo 1) Um polinômio de grau igual a 1, ou também um chamado de monômio:

$a_1x^1+a_0x^0$

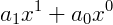
Exemplo 2) Um polinômio de grau igual a 2 ou binômio.

$a_2x^2+a_1x^1+a_0x^0$

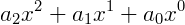
Exemplo 3) Agora um do terceiro grau, ou trinômio, é escrito como:

$a_3x^x+a_2x^2+a_1x^1+a_0x^0$

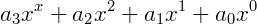
Exemplo 4) A expressão 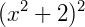$(x^2+2)^2$ é de quarto grau, pois, desenvolvendo o produto temos:

$x^4+4x^2+4$

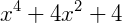
Existem ainda algumas expressões que não podem ser caracterizadas como polinomiais. Para isso, algumas restrições devem ser estabelecidas:

1) O expoente das variáveis x não podem ser negativos:

$x^{-2}+3x^{-1}+1$

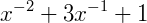
2) A variável x não pode aparecer no denominador de expressões:

$\frac{2}{x^2}+\frac{4}{x}+1$

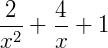
3) Os expoentes não podem ser fracionários e as variáveis não podem aparecer num radical:

$\sqrt{2x}+x^{\frac{3}{2}}+4$

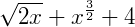
Polinômios completos

São todos aqueles em que a ordem de todos os expoentes da variável 𝑥 estiverem em ordem decrescente, por exemplo:

$3x^3-4x^2+2x-1$

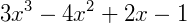
Note que o polinômio acima é do terceiro grau e todos os expoentes de 𝑥 acompanham a sequência (3,2,1,0).

Polinômios incompletos

São aqueles em que faltam algum número na sequência dos expoentes de 𝑥. Ou seja:

$3x^5-4x^3+2x-1$

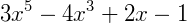
Neste caso, poderíamos completar este polinômio com a sequência correta, mas, para não ocorrer nenhuma alteração na expressão, os coeficientes de 𝑥 que virão a completar o polinômio devem ser iguais a zero, veja:

$3x^5+0x^4-4x^3+0x^2+2x-1$

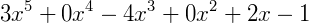
Agora, ele está na ordem que o torna um polinômio completo (5,4,3,2,1,0).

Leia também:

• Adição de polinômios
• Subtração de polinômios
• Divisão de polinômios
• Multiplicação de polinômios
• Função polinomial

Referências Bibliográficas:

DANTE, Luiz Roberto. Matemática: Contexto e Aplicações. Volume 3. São Paulo: Editora Ática, 2011.

GUIDORIZZI, Hamilton L. Um Curso de Cálculo: Volume 1. Rio de Janeiro: Editora LTC, 2001.

Texto originalmente publicado em https://www.infoescola.com/matematica/polinomios/