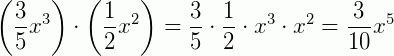Multiplicação de polinômios - Matemática

Dados dois polinômios:

A(x) = a_n xⁿ + a_n-1x^n-1+ ... + a₂x² + a₁x¹ + a_o

B(x) = b_m x^m + b_m-1x^m-1+ ... + b₂x² + b₁x¹ + b_o

existe um único polinômio P(x) tal que

P(x) = A(x) . B(x) para todo 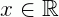$x\in\mathbb{R}$ . Esse polinômio é:

P(x) = (a_n b_m) x^n+m + (a_nb_m-1+ a_n-1b_m)x^n+m-1+ ... + (a₁b_o + a_ob₁))x + (a_o b_o)

e o denominamos produto de A e B. Indicamos: P = A . B

Multiplicação de monômios

Dados dois monômios, semelhantes ou não, podemos sempre obter um novo monômio pela multiplicação deles. Para isso, usamos algumas propriedades da multiplicação e da potenciação.

Veja este exemplo.

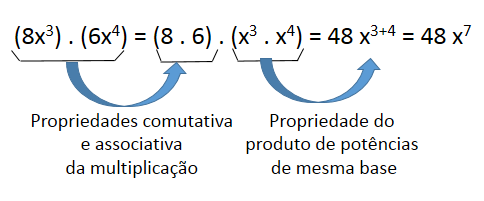
Observe outros exemplos:

(7a) . (-6b) = 7 . (-6) . a. b = -42 ab
(10x) . (5x) = 10 . 5 . x . x = 50 x²
(-y³) . (2 yz) = (-1) . 2 . y³ . y . z = -2y⁴z
(-a) . (-15a³) = (-1) . (-15) . a . a³ = 7a⁴
(5xy) . (2xy²z) = 5 . 2 . x . y . x. y² . z = 10x²y³z
$\left(\frac{3}{5}x^3\right)\cdot\left(\frac{1}{2}x^2\right)=\frac{3}{5}\cdot\frac{1}{2}\cdot x^3\cdot x^2=\frac{3}{10}x^5$

Multiplicação de dois polinômios

Na multiplicação de dois polinômios, devemos multiplicar cada termo de um polinômio por todos os termos do outro e reduzir os termos semelhantes.

Vejam os exemplos:

1) Sendo A = 3x² – 1 e B = x² – 2x + 1. Calcule A.B

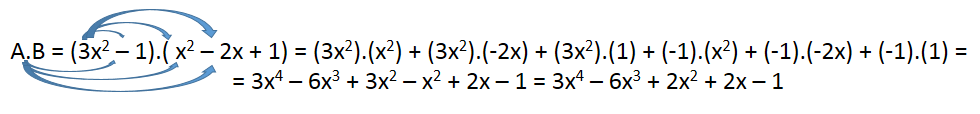
2) Multiplicar A(x) = 2x² – x + 3 por B(x) = x⁵ – x + 1.

Temos:

A(x) . B(x) = (2x² – x + 3).( x⁵ – x + 1) =

(2x²).(x⁵) + (2x²).(-x) + (2x²).(1) + (-x).(x⁵) + (-x).(-x) + (-x). 1 + (3).(x⁵) + (3).(-x) + (3).(1) =

2x⁷ – 2x³ + 2x² –x⁵ – x + 3x⁵ -3x + 3 =

2x⁷ – x⁶ + 3x⁵ –2x³ + 3x² - 3x + 3

3) Multiplicar f(x) = x + 2x² + 3x³por g(x) = 4 + 5x + 6x²

Temos:

f(x) . g(x) = (x + 2x² + 3x³) . (4 + 5x + 6x²) =

(x).(4) + (x).(5x) + (x).(6x²) + (2x²).(4) + (2x²).(5x) + (2x²).(6x²) + (3x³).(4) + (3x³).(5x) + (3x³).(6x²) =

4x + 5x² + 6x³ + 8x² + 10x³ + 12x⁴ + 12x³ + 15x⁴ + 18x⁵ =

18x⁵ + 27x⁴ + 28x³ + 13x²+ 4x

Costuma-se usar o seguinte dispositivo prático:

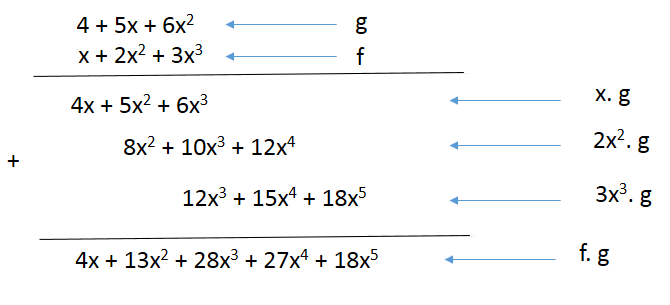
4) Dados A(x) = x³ + 2x + 1 e B(x) = x² – 7x + 2, determinar o polinômio A(x) . B(x).

A(x) . B(x) = (x³ + 2x + 1) . (x² – 7x + 2) =

(x³).(x²) + (x³).(-7x) + (x³).2 + (2x).(x²) + (2x).(-7x) + (2x).2 + 1.x² + 1.(-7x) + 1.2 =

x⁵ – 7x⁴ + 2x³ + 2x³ – 14x² + 4x + x² – 7x + 2 =

x⁵ – 7x⁴ + 4x³ – 9x² – 7x + 2

5) Dados A(x) = 7x³ + 2x² – 5x e B(x) = 2x³ – x² + 7x e C(x) = -x³ – 2x, determinar A(x) . B(x) . C(x).

A(x) . B(x) . C(x) = (7x³ + 2x² – 5x).( 2x³ – x² + 7x).( -x³ – 2x) =

[(7x³ + 2x² – 5x).( 2x³ – x² + 7x)]. ( -x³ – 2x) =

[(7x³).(2x³) + (7x³).(-x²) + (7x³).(7x) + (2x²).(2x³) + (2x²).(-x²) + (2x²).(7x) + (-5x).(2x³) + (-5x).(-x²) + (-5x).(7x)]. ( -x³ – 2x) =

[14x⁶ – 7 x⁵ + 49 x⁴ + 4x⁵ - 2x⁴ + 14x³ - 10x⁴ + 5x³ - 35x²].( -x³ – 2x) =

[14x⁶ + 2x⁵ + 37x⁴ + 19x³ – 35x²].( -x³ – 2x) =

(14x⁶).(-x³) + (14x⁶).(-2x) + (-3x⁵).(-x³) + (-3x⁵).(-2x) + (37x⁴).(-x³) + (37x⁴).(-2x) + (19x³).(-x³) + (19x³).(-2x) + (-35x²).(-x³) + (-35x²).(-2x) =

-14x⁹ – 28x⁷ + 3x⁸ – 4x⁶ – 37x⁷ – 64x⁵ – 19x⁶ – 38x⁴ + 35x⁵ + 70x³ =

-14x⁹ + 3x⁸– 65x⁷ – 23x⁶ - 29x⁵ – 57x⁵ – 38x⁴ + 70x³

Aplicações práticas

Podemos usar os polinômios para expressar algebricamente áreas e volumes de figuras planas. Vejam os exemplos:

1) No retângulo a seguir as medidas dos lados estão na mesma unidade de medida. Escreva a expressão que representa a área da região.

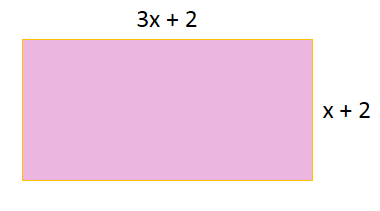
A área de um retângulo é dada pelo produto do comprimento pela largura.

A(x) = (3x + 2).(x + 2) =

(3x).(x) + (3x).(2) + (2).(x) + (2).(2) =

3x² + 6x + 2x + 4 =

3x² + 8x + 4

2) A figura abaixo representa um cubo de lados (x – 3). Escreva a expressão que representa o volume desse sólido geométrico.

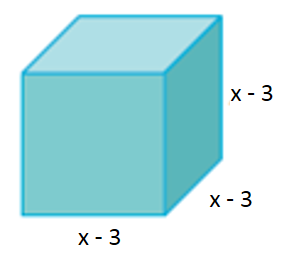
O volume de um cubo é dado pelo produto do comprimento pela largura e pela altura.

V(x) = (x – 3).(x - 3).(x – 3) = [(x – 3).(x - 3)].(x – 3) =

= [x.x + (x).(-3) + (-3).x + (-3).(-3)].(x – 3) =

= [x² - 3x -3x + 9]. (x – 3) = [x² – 6x + 9].(x – 3) =

= (x²).x + (x²).(-3) + (-6x).x + (-6x).(-3) + 9.x + 9.(-3) =

= x³ – 3x² – 6x² + 18x + 9x – 27 = x³ – 9x² + 27x - 27