Segunda Lei de Kepler - Lei das Áreas - Astrofísica

Ouça este artigo:

Das três notáveis contribuições que o astrônomo e matemático alemão Johannes Kepler (1571-1630) deu à astronomia moderna, aquela que ficou famosa como a Segunda Lei de Kepler, na verdade, a primeira a ser obtida. Meses antes de descobrir o formato preciso das trajetórias planetárias em sua primeira lei, Kepler chegou a um resultado surpreendente ao estudar as órbitas da Terra e de Marte a partir da extensa coleção de dados que herdou do astrônomo dinamarquês Tycho Brahe (1546-1601).

Ao procurar por alguma proporcionalidade entre a velocidade orbital da Terra e sua distância ao Sol, Kepler chegou a uma relação curiosa entre a área “varrida” por uma linha imaginária ligando o planeta ao Sol e o tempo gasto no percurso orbital correspondente. Aplicando seus resultados aos dados sobre Marte, sua descoberta, além de confirmada, foi crucial na elucidação do enigma do formato daquela e das demais órbitas do Sistema Solar. Em suas anotações, escreveu: “o tempo para um planeta descrever um arco infinitesimal é proporcional à sua distância ao Sol”. Em linguagem moderna, a hoje denominada segunda lei de Kepler para o movimento planetário, também conhecida como “lei das áreas”, pode ser assim enunciada:

A reta que une um planeta ao Sol varre áreas iguais em intervalos de tempo iguais.

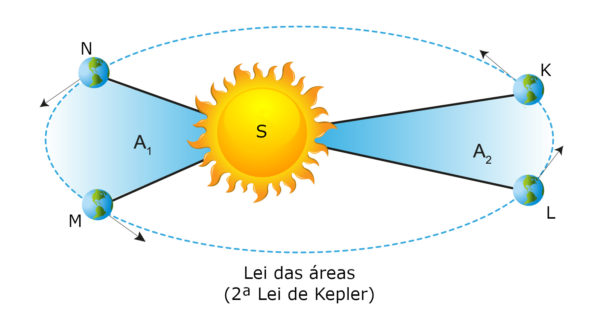
Figura 1. Áreas correspondentes em diferentes trechos do plano orbital de um planeta.
Representação artística, não em escala. Ilustração: Emir Kaan / Shutterstock.com

Na Figura 1, está ilustrada a órbita de um planeta em torno do Sol, na qual se destacam duas áreas iguais, em verde, internas à elipse. Em um dado intervalo de tempo, digamos ∆t_KL, o planeta se desloca do ponto K ao ponto L, e a linha imaginária que o liga ao Sol varre a área KSL. Em outro intervalo, ∆t_MN, o planeta se desloca de M a N, e a mesma linha imaginária que o liga ao Sol varre a área MSN. Aplicada a essa órbita, a segunda lei de Kepler implica que:

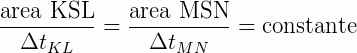
$\frac{\text{area KSL}}{\Delta t_{KL}}=\frac{\text{area MSN}}{\Delta t_{MN}}=\text{constante}$

Como as áreas destacadas na ilustração são iguais, a aplicação da lei conduz à conclusão de que ∆t_KL = ∆t_MN, o que significa que o intervalo de tempo necessário para que o planeta se desloque no trecho da órbita de K a L é também o intervalo necessário para que ele se desloque de M a N. Sendo trechos de tamanhos distintos, como demonstra a figura, o fato de o tempo gasto neles pelo planeta ser o mesmo denota que a velocidade orbital assume valores diferentes em diferentes pontos da órbita.

E é este o significado físico da segunda lei de Kepler: a velocidade orbital de um planeta não é uniforme, mas varia regularmente ao longo da órbita. O que é constante é a chamada velocidade areal, ou velocidade areolar, que é justamente definida como a área varrida pela linha que une o planeta ao Sol por unidade de tempo (matematicamente, a quantidade representada por cada uma das frações da equação acima).

Na ilustração, os pontos foram convenientemente escolhidos para delimitar os trechos da órbita em torno do ponto de maior proximidade do planeta em relação ao Sol (arco MN, em torno do periélio) e do ponto da órbita mais afastado do Sol (arco KL, em torno do afélio). Da conclusão de que os intervalos de tempo para percorrer ambos os arcos são idênticos, é fácil perceber que a velocidade orbital do planeta é maior no periélio, quando está mais próximo do Sol, que no afélio, quando está mais afastado.

É importante registrar que há interessantes analogias que lançam mão de conceitos relacionados à gravitação ou à conservação de momento angular como justificativa teórica para a segunda lei de Kepler. Elas, contudo, devem ser percebidas apenas como artifícios úteis para que se entenda a natureza física por trás dessa propriedade do movimento planetário. Kepler, por sua vez, desenvolveu suas ideias em período imediatamente anterior ao advento da mecânica newtoniana, de modo empírico, e não possuía intenção de identificar a causa do que constatava. Sua motivação era descrever, em termos de um padrão generalizado, o que observava no abundante conjunto de dados de que dispunha sobre o Sistema Solar.