Quando estudamos função, verificamos que uma função do 1º grau é definida por uma expressão polinomial do 1º grau com duas variáveis que o seu gráfico é uma reta.
Reciprocamente, podemos dizer que uma linha reta é representada por uma equação do 1º grau com duas variáveis.
Nesta unidade, estudaremos essa representação.
Conteúdo deste artigo
Equação fundamental da reta
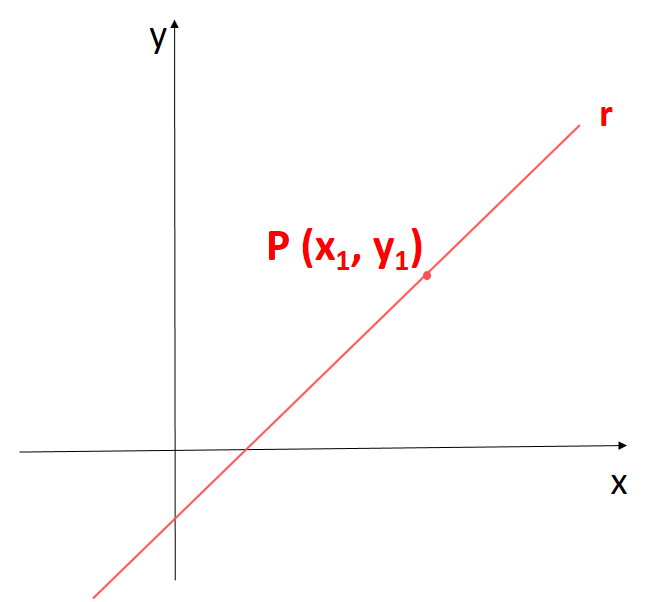
Equação de uma reta que passa por um ponto P(x1, y1) e cujo coeficiente angular é m.
Consideremos uma reta r que passa pelo ponto P(x1, y1) e tem coeficiente angular m.
Observação: Vale lembrar que o coeficiente angular de uma reta é a medida da tangente do ângulo que a reta forma com o eixo x, no sentido anti-horário.
Mantendo o ponto Q (x, y) sobre a reta r, com Q ≠ P, vamos determinar a equação que representa a reta que passa por esses dois pontos.
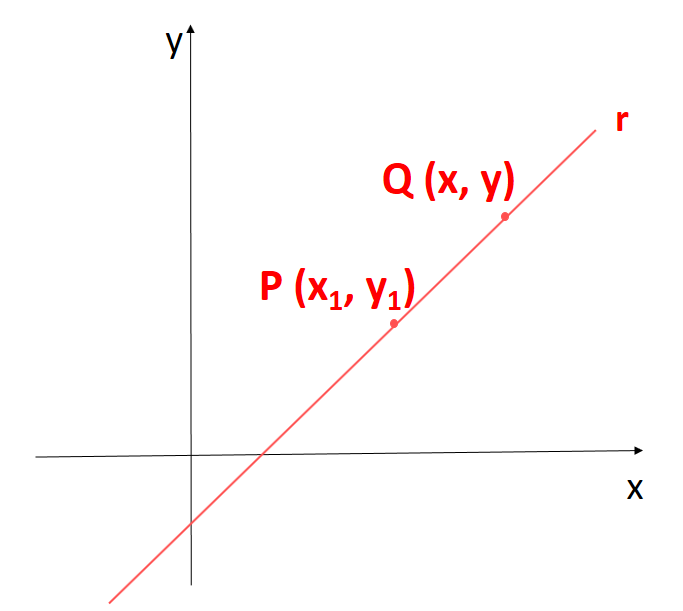
Utilizando a fórmula do coeficiente angular, temos:
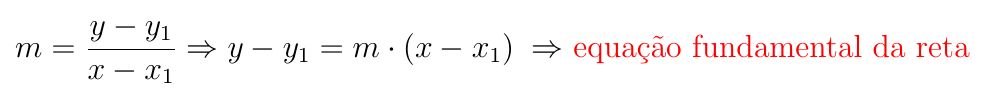
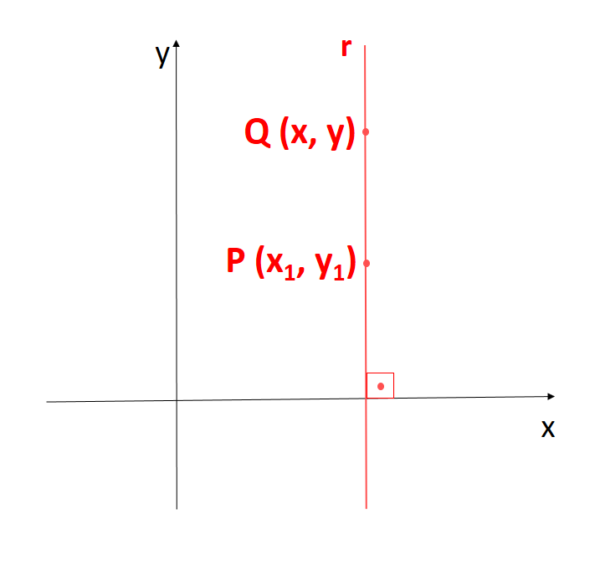
Observação: Se a reta r é vertical, então todos os pontos da reta têm a mesma abscissa. Assim, o ponto Q (x, y) é um ponto qualquer da reta se, e somente se x = x1.
Equação reduzida da reta
Já sabemos que a equação da reta, se forem conhecidos um ponto P(x1, y1) da reta e o coeficiente angular m, é dada por:
![]()
Se escolhermos o ponto particular de coordenadas (0, n) para o ponto (x1, y1), teremos a equação:
![]()
![]()
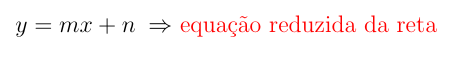
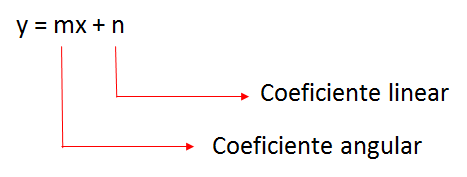
O número real n, que é a ordenada do ponto onde a reta corta o eixo y, é chamado coeficiente linear da reta.
Então:
Equação segmentária da reta
Consideremos uma reta r, tal que:
- r intercepta o eixo x no ponto A (p, 0);
- r intercepta o eixo y no ponto B (0, q).
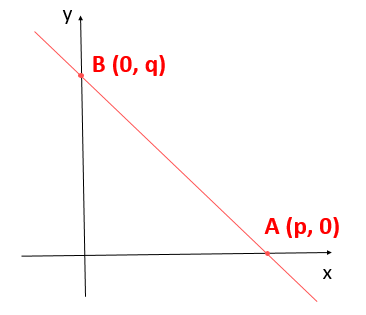
Então:
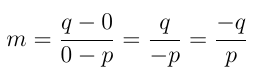
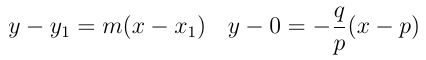
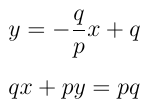
Dividindo ambos os membros por pq, se p ≠ 0 e q ≠ 0, temos:
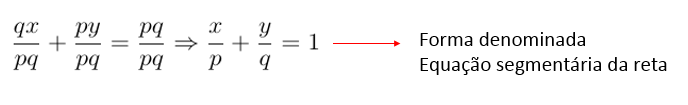
Equação geral da reta
Consideremos a reta r indicada na figura e os pontos A (x1, y1) e B(x2, y2) sobre ela.
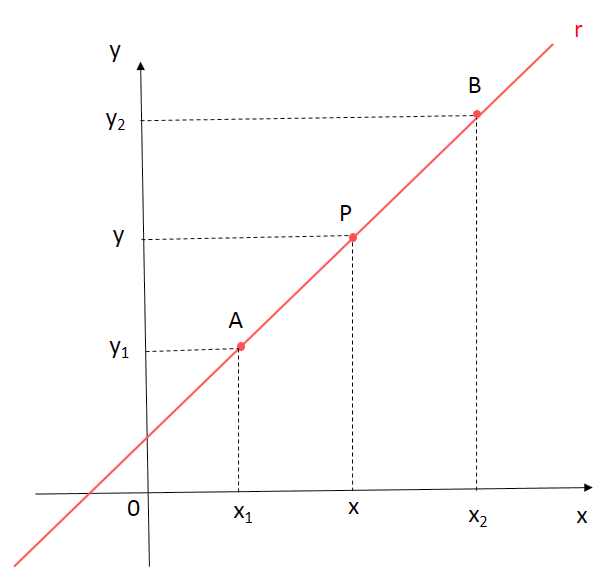
Seja P (x, y) um ponto qualquer dessa reta.
Se os pontos P, A e B são colineares, temos:
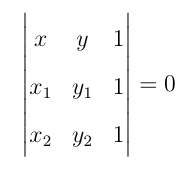
Desenvolvendo o determinante, temos:
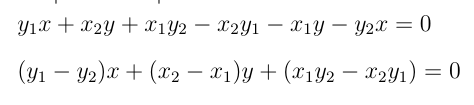
Fazendo
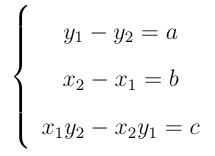
obtemos a equação geral da reta
ax + by + c = 0
com a, b e c constantes.
Referências bibliográficas:
1. MURAKAMI, C.; IEZZI, G. Fundamentos de Matemática Elementar: Conjuntos. Funções. Vol. 1. 8ª Ed. Editora: Atual. 2004.
2. LIMA, E. L., et al. A Matemática do Ensino Médio. 9ª ed. Rio de Janeiro: SBM, 2006. v.1
3. DANTE, Luis Roberto. Matemática: contexto e aplicações. Volume único. São Paulo: Editora Ática, 2009.
Texto originalmente publicado em https://www.infoescola.com/matematica/equacao-da-reta/