É chamada de matriz uma tabela retangular composta por escalares, onde chamamos estes escalares de entradas ou elementos. Inicialmente, apresentaremos alguns exemplos importantes sobre matrizes de forma generalizada.
De uma forma geral, seja uma matriz A, podemos representá-la como:
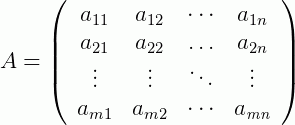
Onde m é o número de linhas e n o número de colunas de uma matriz. Note que o elemento aij, também chamado de ij-ésima entrada simboliza a posição deste elemento dentro da matriz, ou seja, a11 está posicionado na 1ª linha e na 1ª coluna. O a21 está na 2ª linha e na 1ª coluna e assim por diante. Uma matriz também pode ser representada da forma compacta:
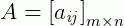
Dizemos que uma matriz com m linhas e n colunas é uma matriz m por n, onde escrevemos m x n na notação acima. Vejamos alguns exemplos:
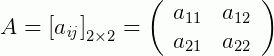
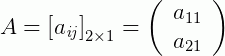
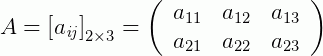
Conteúdo deste artigo
Matriz Linha
É chamada de matriz linha, aquela que é composta apenas por uma linha, ou seja, m=1. De modo geral:
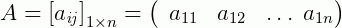
Matriz Coluna
A matriz coluna, como diz o nome, é composta apenas por uma coluna. Sendo assim, n=1:
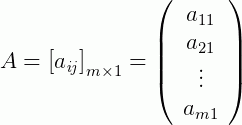
Matriz Quadrada
Dizemos que é quadrada a matriz onde o número de linhas é igual ao de colunas, m=n. Neste caso, podemos representar de forma compacta:
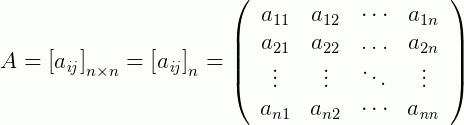
Onde n é chamado de ordem da matriz. Note que se o termo “ordem da matriz” é utilizado, então necessariamente ela é quadrada. Vejamos alguns exemplos:
1 - Se uma matriz é dita de ordem 2, isto significa que ela possuirá 2 linhas e duas colunas:
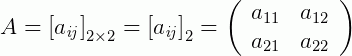
2 - Agora, uma matriz de ordem 3 terá 3 linhas e 3 colunas:
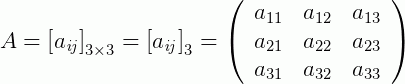
Matriz Nula
Uma matriz nula é uma matriz, de qualquer dimensão ou ordem, onde todos os seus elementos são compostos apenas por zeros, ou seja:
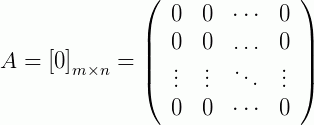
Matriz Diagonal
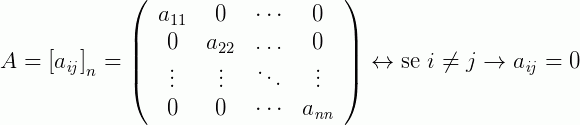
A matriz diagonal é aquela, seja de qualquer ordem (quadrada), onde os elementos que não compõe a diagonal principal, são zeros. Isto é, seja a matriz 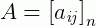 , se
, se 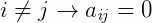 , logo:
, logo:
Matriz Identidade ou Unitária
A matriz identidade, simbolizada por I, é uma matriz diagonal onde os seus elementos da diagonal principal são compostos apenas pelo número 1:
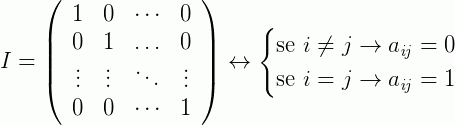
Notação Importante
Quando escrevemos uma matriz, podemos usar dois símbolos diferentes: As chaves (como em todos os exemplos acima) ou os colchetes:
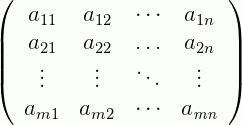
ou
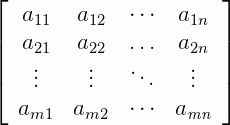
É comum ver uma “matriz” representada da forma abaixo em alguns livros, com duas barras ao invés de chaves ou colchetes.
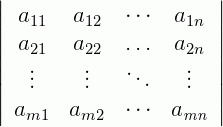
Mas cuidado, esta notação é usada apenas quando nos referimos ao determinante da matriz ali escrita entre as barras e não para uma matriz propriamente dita.
Formando uma Matriz
Vamos agora criar uma matriz usando uma lei que determinará o valor de suas entradas (elementos) a partir da relação enunciada abaixo:
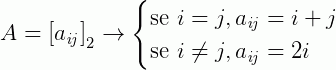
Note, nesta lei de formação estamos usando os valores de cada posição do elemento (linha e coluna) como fatores que vão determinar qual será o número que a matriz irá atribuir em cada posição correspondente, ou seja:
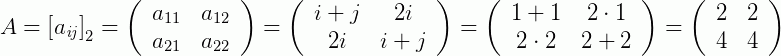
Agora, outro exemplo:
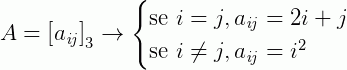
Isso nos dá,
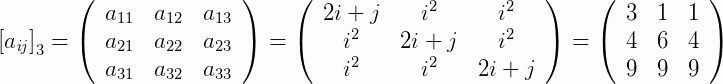
Leia também
- Operações com Matrizes (matriz transposta, adição, subtração, oposta)
- Multiplicação de matrizes
- Multiplicação de um número real por uma matriz
- Matriz Identidade
- Transposição de Matrizes
- Adição e subtração de Matrizes
- Matriz transposta
- Matriz inversa
- Matriz adjunta
- Igualdade de matrizes
Referências bibliográficas:
ARFKEN, George B; WEBER, Hans J; HARRIS, Frank E. '''Física Matemática: Métodos Matemáticos para Engenharia e Física – 7ª Ed'''. Rio de Janeiro: Elsevier, 2017.
LIPSCHUTZ, Seymor; LIPSON, Marc. '''Álgebra Linear – 4ª Ed'''. Porto Alegre: Bookman, 2011.
Texto originalmente publicado em https://www.infoescola.com/matematica/matrizes/
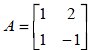 , seja a matriz B tal que A-1BA = D onde
, seja a matriz B tal que A-1BA = D onde