Geometria Plana

A geometria plana estuda o comportamento de estruturas no plano, a partir de conceitos básicos primitivos como ponto, reta e plano. Estuda o conceito e a construção de figuras planas como quadriláteros, triângulos, círculos, suas propriedades, formas, tamanhos e o estudo de suas áreas e perímetro.

Conceitos básicos

Os conceitos básicos, ou primitivos, da geometria plana, são chamados de axiomas, ou seja, são aceitos sem demonstrações. São apenas noções que auxiliam no entendimento de conceitos mais completos.

Ponto

Segundo “Os Elementos”, de Euclides, um ponto é definido como "o que não tem partes". É apenas uma posição no espaço. É representado por letras maiúsculas.

Reta

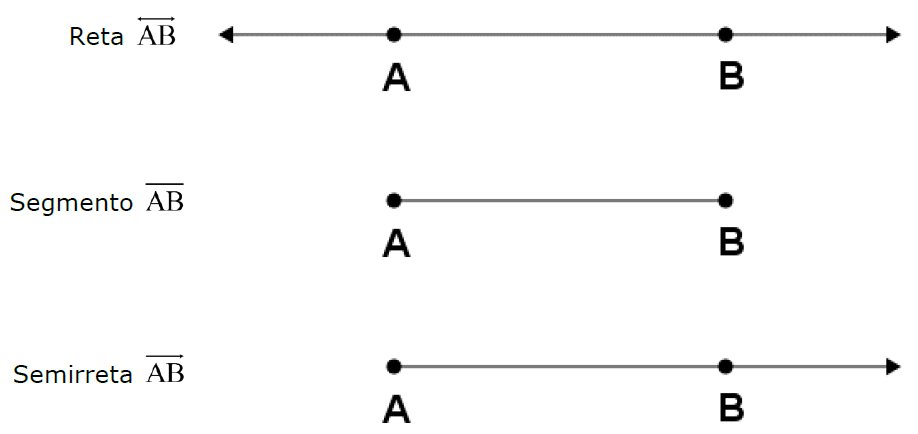
Uma reta é a reunião de infinitos pontos. É uma “linha” com comprimento, mas sem largura. É sempre representada por uma letra minúscula.

Se tivermos dois pontos, eles determinam uma reta. Há apenas uma reta que passa por esses dois pontos. Por um ponto passam infinitas retas.

Duas retas são concorrentes se, e somente se, elas têm um único ponto em comum.

Plano

Um plano é uma região onde há infinitos pontos e infinitas retas. É um elemento com comprimento e largura. Geralmente é representado por letras gregas.

Um plano é determinado por três pontos não colineares (pontos não alinhados). Se uma reta tem dois pontos distintos em um plano, então esta reta está contida nesse plano.

Segmento de Reta

Dados dois pontos distintos A e B, a união desses pontos com o conjunto de pontos compreendidos entre A e B é chamado de segmento de reta.

Representamos esse segmento de reta AB por $\overline{AB}$ .

Semirreta

Dados dois pontos distintos A e B, a reunião do segmento de reta $\overline{AB}$ com o conjunto dos pontos X tais que B está entre A e X é a semirreta AB, indicada por $\overrightarrow{AB}$ .

Em resumo, temos:

Ângulos

Chama-se ângulo a região entre duas semirretas que partem de uma mesma origem. Podemos dizer, ainda que um ângulo é a medida da abertura de duas semirretas que partem da mesma origem.

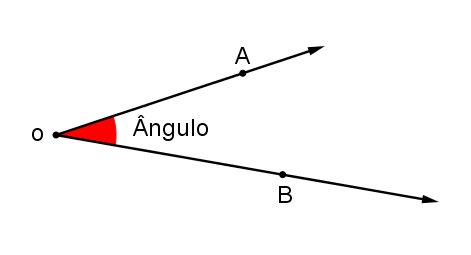
Indica-se: ∠AOB, ∠BOA, AÔB, BÔA ou Ô.

O ponto O é o vértice do ângulo e as semirretas $\overline{OA}$ e $\overline{OB}$ são os lados do ângulo.

Polígonos

Polígonos são figuras geométricas planas que são formadas por segmentos de reta a partir de uma sequência de pontos de um plano, todos distintos e não colineares, onde cada extremidade de qualquer um desses segmentos é comum a apenas um outro.